Chapter 11 범주형 변수에 대한 가설검정

이 장에서는 R을 이용하여 범주형 변수에 대해 가설검정하는 방법을 알아본다.

11.1 단일 모집단의 모비율에 대한 가설검정

모집단이 하나일 때, 특정 범주가 차지하는 비율 \(p\)에 대해 가설검정하는 방법을 살펴보자. 모집단에서의 관심의 대상이 되는 범주의 비율 \(p\)를 모비율이라고 한다. 여기서 관심의 대상이 되는 범주는 문제마다 다르게 정의될 수 있다. 모비율이 어떤 전염병에 대한 항체 보유자에 대한 비율일 수도 있고, 어떤 정단에 대한 지지율일 수도 있다.

가설검정을 위해 모집단에서 \(n\) 개의 표본을 추출하였다고 하자. 그 중 \(x\) 개가 해당 범주의 관측도수라면 표본비율 \(\hat{p}\)은 다음과 같이 계산된다.

\[ \hat{p} = x / n. \]

단일 모집단의 모비율에 대한 가설검정에서 귀무가설은 모집단의 비율 \(p\)가 특정값 \(p_0\)이다로 설정된다. 반면 대립가설은 모비율 \(p\)가 \(p_0\)가 아니다, 더 크다, 더 작다 중 하나로 설정된다. 앞서 보았던 Example 10.1의 동전의 앞면이 나올 비율에 대한 가설검은 단일 모집단의 모비율에 대한 가설검정의 예라 할 수 있다.

모비율에 대한 가설검정은 검정통계량과 표본분포로 다음 두 가지 중 하나가 사용된다.

• 이항분포로 검정: 가설검정에 사용할 검정통계량으로 표본에서의 특정 범주가 관측된 수 \(x\)를 사용한다. 그러면 모집단의 크기가 크고 표본의 선택이 서로 독립이라면 검정통계량 \(x\)는 모비율이 \(p = p_0\)라는 귀무가설 하에 이항분포 \(Binom(n, p_0)\)를 따른다.

\[ x \sim Binom(n, p_0). \]

• 정규분포로 검정: 검정통계량으로 표본비율 \(\hat{p}\)을 사용하다. 그러면 \(\hat{p}\)은 모비율이 \(p = p_0\)라는 귀무가설 하에 정규분포 \(N(p_0, \sqrt{p_0(1-p_0)/n})\)을 근사적으로 따른다. 따라서 다음과 같이 표준정규분포를 따른는 검정통계량 \(T\)를 사용하여 가설검정을 수행한다.

\[ T = \frac{\hat{p} - p_0}{\sqrt{\frac{p_0(1 - p_0)}{n}}} \sim N(0, 1) \]

이항분포 검정은 표본의 추출이 독립적이라는 가정 하에 정확한 확률분포이고, 정규분포 검정은 검정통계량에 대한 근사적 확률분포이므로 가능하면 이항분포 검정을 사용하는 것이 좋다. 그러나 예전에는 컴퓨터의 계산 능력이 높지 않았기 때문에 비율 검정을 사용하는 경우가 많았다. 다만 \(n\)이 매우 크고 \(np\)의 값이 충분히 큰 경우에는 이항분포 검정이나 정규분포 검정의 차이가 거의 없다. 이 경우에는 계산 시간의 절약을 위하여 정규분포 검정을 사용할 수 있다.

대립가설에 따라 기각역의 위치는 다음과 같이 정리될 수 있다.

귀무가설 (\(H_0\))	대립가설 (\(H_1\))	기각역의 위치
\(p = p_0\)	\(p \neq p_0\)	양측검정
\(p = p_0 \, (p \ge p_0)\)	\(p < p_0\)	왼쪽 단측검정
\(p = p_0 \, (p \le p_0)\)	\(p > p_0\)	오른쪽 단측검정

왜냐하면 대립가설이 \(p < p_0\)가 채택되려면 표본의 관측도수 \(x\)가 귀무가설이 맞다고 했을 때의 이항분포에서 예외적으로 작게 나와야 한다. 그러므로 분포의 왼쪽을 기각역으로 설정하는 왼쪽 단측검정을 한다. 마찬가지로 대립가설이 \(p > p_0\)가 채택되려면 관측도수 \(x\)가 귀무가설 하의 이항분포에서 예외적으로 크게 나와야 한다. 그러므로 분포의 오른쪽을 기각역으로 설정하는 오른쪽 단측검정을 한다. 대립가설이 \(p \neq p_0\)이면 관측도수 \(x\)가 귀무가설 하의 이항분포에서 예외적으로 작거나 크게 나올 때 대립가설을 채택하므로, 기각역은 분포의 양쪽에 모두 있게 된다. 같은 방식으로 표본비율 \(\hat{p}\)의 값이 대립가설이 받아들여지려면 귀무가설의 모비율 \(p_0\)보다 작아야 하는지, 커야 하는지를 생각해 보면 기각역의 위치가 위의 표처럼 되는 것을 쉽게 이해할 수 있다.

11.1.1 binom.test()로 단일 모집단 모비율 검정하기

R의 기본 패키지인 stat 패키지의 binom.test() 함수는 이항분포를 사용하여 단일 모집단에 대한 모비율에 대한 가설검정을 수행한다.

binom.test() 함수를 이용하여 단일 모집단의 모집율에 대한 가설검정을 하는 문법은 다음과 같다.

binom.test(x = 관측도수, n = 표본수, p = 귀무가설_모비율, alternative = "대립가설_종류")
binom.test(x = 관측도수, n = 표본수, p = 귀무가설_모비율, 
    alternative = "대립가설_종류", conf.level = 신뢰수준)  # 신뢰구간의 신뢰수준을 조정

binom.test() 함수에 사용되는 인수는, stat 패키지의 가설검정 함수들이 공통적으로 사용하는 인수도 있고, 모비율 검정에만 관련된 인수가 있다. binom.test()의 처음 세 인수는 모비율 검정에만 관련된 인수이다.

• x: 표본에서 특정 범주가 발생한 횟수
• n: 표본의 크기
• p: 귀무가설의 모비율 \(p_0\)

그 다음의 두 인수는 stat 패키지의 가설검정 함수들이 공통적으로 사용하는 인수이다.

• alternative: 대립가설의 종류를 지정한다. 대립가설이 \(p \neq p_0\)이면 양측 검정을 의미하는 "two.sided"로, \(p < p_0\)이면 왼쪽 검증을 의미하는 "less"로, \(p > p_0\)이면 오른쪽 검정을 의미하는 "greater"로 값을 입력한다.
• conf.level: 대부분의 가설검정 함수는 신뢰구간도 함께 알려주는데 이 인수는 신뢰구간의 신뢰수준을 지정한다. 기본값은 0.95로 95% 신뢰구간을 계산하여 알려준다.

Example 11.1 어떤 회사 제품의 불량률이 10%였다고 하자. 새로운 공정을 도입한 후 300개의 제품을 생산한 후 불량품을 조사하였더니 20개가 발견되었다. 새로운 공정 도입으로 불량률이 저하되었는지 유의수준 5%에서 가설검정하시오.

Example 11.1의 가설검정은 불량률이 감소했다는 것을 검정하고자 하는 것이다. 그러므로 \(p\)를 새 공정의 불량률이라고 하면 귀무가설과 대립가설은 다음과 같이 설정한다. 왜냐하면 귀무가설은 일반적으로 받아들여지는 가설이다. 이 예에서 지금까지의 불량률이 10%였으므로 특별한 증거가 있지 않다면 새로운 공정의 불량률도 10%라고 생각하는 것이 합리적이다. 대립가설은 표본에서 특별한 증거가 발생하면 채택하고자 하는 가설이 된다.

\[ \begin{align} H_0: & \quad p = 0.1 \\ H_1: & \quad p < 0.1 \end{align} \]

binom.test()을 사용하여 가설검정을 하면 다음과 같은 결과를 얻는다.

> binom.test(x = 20, n = 300, p = 0.1, alternative = "less")

    Exact binomial test

data:  20 and 300
number of successes = 20, number of trials = 300, p-value = 0.02868
alternative hypothesis: true probability of success is less than 0.1
95 percent confidence interval:
 0.00000000 0.09540198
sample estimates:
probability of success 
            0.06666667 

인수들을 순서에 맞게 기술하면 인수의 이름을 생략하거나 일부만 기술해도 된다. 인수의 이름을 기술하면 순서는 중요하지 않다. 다음 명령문은 모두 동일한 결과를 준다.

> binom.test(20, 300, p = 0.1, alternative = "less")
> binom.test(20, 300, 0.1, "less")
> binom.test(p = 0.1, alternative = "less", x = 20, n = 300)

이항분포 검정을 통해 우리는 다음 사실을 알 수 있다.

• 표본 비율 \(\hat{p}\)는 0.0666667이다.
• p-값은 0.028679로 유의수준 0.05에서 귀무가설을 기각한다. (대립가설을 채택한다.)

Example 11.2 bizstatp 패키지의 course 데이터는 어떤 과목의 수강생에 대한 정보이다. 이 과목은 평균적으로 수강생의 여학생 비율이 30%였다.
현재 이 과목 수강생의 여학생 비율의 과거와 달라졌다고 볼 수 있는지 유의수준 5%에서 가설검정하시오. (bizstatp 패키지의 설치 방법과 course 데이터에 대한 설명은 6.3 절을 참조한다.)

Example 11.2의 가설검정은 여학생의 비율이 달라졌는지를 검정하는 것이다. \(p\)를 수강생 중 여학생의 비율이라고 하면 귀무가설과 대립가설을 다음과 같이 설정한다.

\[ \begin{align} H_0: & \quad p = 0.3 \\ H_1: & \quad p \neq 0.3 \end{align} \]

binom.test()을 사용하여 가설검정을 하려면, x와 n의 값을 구해야 한다. Example 11.2에서는 x는 여학생의 수, n은 전체 수강생이 된다. 이를 구하기 위해서는 성별 수강생의 빈도표가 필요하다.

> library(bizstatp)
> head(course)

   major year gender class mid final   hw score
1 Others    4      M     1  62    66 83.6 73.47
2 Others    3      F     1  46    37 88.7 61.50
3     ME    2      M     1  94    82 87.9 89.18
4     ME    2      M     1  73    71 88.7 78.47
5     ME    2      M     1  96    93 90.6 93.88
6     ME    2      M     1  54    43 84.3 64.39

> tg <- xtabs(~ gender, data = course)
> tg

gender
 F  M 
18 27 

x는 빈도표의 첫번째 요소이고 n은 빈도표의 모든 관측도수를 합하면 구할 수 있다. 그러므로 이 값을 binom.test()에 입력하면 다음 결과를 얻는다..

> binom.test(tg[1], sum(tg), p = 0.3, alternative = "two.sided")

    Exact binomial test

data:  tg[1] and sum(tg)
number of successes = 18, number of trials = 45, p-value = 0.1457
alternative hypothesis: true probability of success is not equal to 0.3
95 percent confidence interval:
 0.2569759 0.5566865
sample estimates:
probability of success 
                   0.4 

이항분포 검정을 통해 우리는 다음 사실을 알 수 있다.

• 표본 비율 \(\hat{p}\)는 0.4이다.
• p-값은 0.1457496로 유의수준 0.05에서 귀무가설을 채택한다. (대립가설을 기각한다.)
• 모비율의 95% 신뢰구간은 0.2569759에서 0.5566865이다.

Example 11.3 course 데이터는 어떤 과목의 수강생에 대한 정보이다. 이 과목은 과거에 평균적으로 수강생 중 2학년 학생의 비율이 80%였다.
현재 이 과목의 2학년 학생의 수강 비율이 과거보다 줄었다고 볼 수 있는지 유의수준 5%에서 가설검정하시오.

Example 11.3의 가설검정은 2학년 학생의 수강 비율이 줄어들었는지를 검정하고자 하는 것이다. \(p\)를 2학년 학생의 수강 비율이라고 하면 귀무가설과 대립가설은 다음과 같이 설정한다.

\[ \begin{align} H_0: & \quad p = 0.8 \\ H_1: & \quad p < 0.8 \end{align} \]

binom.test()를 이용하여 가설검정을 하려면 먼저 빈도표를 구해야 한다. 범주형 변수의 범주가 세 개 이상인 경우 빈도표를 이용하여 가설검정할 때, 범주표에서 x의 위치를 정확히 지정하여야 한다. 이 예에서는 2학년 학생의 수는 빈도표의 2번째 요소이다. n은 전체 관측도수의 합으로 구하면 된다.

> ty <- xtabs(~ year, data = course)
> ty

year
 1  2  3  4 
 1 32  9  3 

> binom.test(ty[2], sum(ty), p = 0.8, alternative = "less")

    Exact binomial test

data:  ty[2] and sum(ty)
number of successes = 32, number of trials = 45, p-value = 0.09945
alternative hypothesis: true probability of success is less than 0.8
95 percent confidence interval:
 0.0000000 0.8198828
sample estimates:
probability of success 
             0.7111111 

이항분포 검정을 통해 우리는 다음 사실을 알 수 있다.

• 표본 비율 \(\hat{p}\)는 0.7111111이다.
• p-값은 0.0994542로 유의수준 0.05에서 귀무가설을 채택한다. (대립가설을 기각한다.)

11.1.2 빈도표를 입력변수로 전달하기

범주형 변수를 빈도표로 요약한 후 가설검정하는 경우가 빈번하기 때문에 binom.test()와 뒤에서 볼 prop.test()는 첫번째 인수로 빈도표를 입력받아 가설검정을 수행할 수 있다. 빈도표를 직접 입력받아 가설검정할 때, binom.test()와 prop.test()는 빈도표의 첫번째 범주에 대한 비율에 대하여 가설 검정을 수행한다.

> tg

gender
 F  M 
18 27 

> binom.test(tg, p = 0.3, alternative = "two.sided")

    Exact binomial test

data:  tg
number of successes = 18, number of trials = 45, p-value = 0.1457
alternative hypothesis: true probability of success is not equal to 0.3
95 percent confidence interval:
 0.2569759 0.5566865
sample estimates:
probability of success 
                   0.4 

이 경우 빈도표는 성별의 빈도표처럼 두 개의 범주로만 이루어져 있어야 한다. 학년의 빈도표처럼 3 개 이상의 범주가 있으면 앞에서 설명한 것처럼 직접 x와 n 인수를 각각 빈도표에서 지정하여 입력하여야 한다.

> ty

year
 1  2  3  4 
 1 32  9  3 

> binom.test(ty, p = 0.8, alternative = "less")

Error in binom.test(ty, p = 0.8, alternative = "less"): incorrect length of 'x'

11.1.3 prop.test()로 단일 모집단 모비율 검정하기

prop.test() 함수는 정확한 이항분포 대신 근사적인 표준정규분포를 이용하여 가설검정을 수행한다. 단일 모집단의 모비율에 대한 가설검정의 경우 prop.test()의 인수의 사용방법은 binom.test()와 동일하다.

다음은 Example 11.1 문제를 prop.test() 함수를 이용하여 가설검정을 수행한 결과이다. binom.test()에서 검정통계량만 달라지므로 귀무가설과 대립가설은 모두 동일하다.

> prop.test(20, 300, p = 0.1, alternative = "less")

    1-sample proportions test with continuity correction

data:  20 out of 300, null probability 0.1
X-squared = 3.3426, df = 1, p-value = 0.03375
alternative hypothesis: true p is less than 0.1
95 percent confidence interval:
 0.00000000 0.09635565
sample estimates:
         p 
0.06666667 

비율 검정을 통해 우리는 다음 사실을 알 수 있다.

• 표본 비율 \(\hat{p}\)는 0.0666667이다. (이항분포 검정과 동일하다.)
• p-값은 0.0337541로 유의수준 0.05에서 귀무가설을 기각한다. (대립가설을 채택한다.) p-값은 이항분포 검정과 조금 다른 것을 볼 수 있다. 비율 검정은 근사치로 분포를 계산하므로 n이 매우 크지 않으면 정확한 검정인 이항분포 검정과는 차이가 발생한다.
• 모비율의 95% 신뢰구간은 0에서 0.0963556이다. 신뢰구간도 사용되는 추정 통계량이 다르므로 이항분포 검정의 결과와는 조금 값이 다르다.

다음은 Example 11.2 문제를 prop.test() 함수를 이용하여 비율 검정을 수행한 결과이다. 이 문제도 검정통계량만 달라지므로 귀무가설과 대립가설은 모두 동일하다.

> prop.test(tg, p = 0.3, alternative = "two.sided")

    1-sample proportions test with continuity correction

data:  tg, null probability 0.3
X-squared = 1.6931, df = 1, p-value = 0.1932
alternative hypothesis: true p is not equal to 0.3
95 percent confidence interval:
 0.2606306 0.5562701
sample estimates:
  p 
0.4 

비율 검정을 통해 우리는 다음 사실을 알 수 있다.

• 표본 비율 \(\hat{p}\)는 0.4이다. (이항분포 검정과 동일하다.)
• p-값은 0.19319로 유의수준 0.05에서 귀무가설을 채택한다. (대립가설을 기각한다.) p-값은 이항분포 검정과 조금 다른 것을 볼 수 있다. 비율 검정은 근사치로 분포를 계산하므로 n이 매우 크지 않으면 정확한 검정인 이항분포 검정과는 차이가 발생한다.
• 모비율의 95% 신뢰구간은 0.2606306에서 0.5562701이다. 신뢰구간도 사용되는 추정 통계량이 다르므로 이항분포 검정의 결과와는 조금 값이 다르다.

11.1.4 정규분포를 이용한 비율 검정에서 연속성 수정

prop.test() 함수는 binom.test() 함수보다 correct라는 인수를 하나 더 가지고 있다. 범주형 변수의 발생 건수 x는 0 또는 자연수의 값을 가지므로 이산형 확률변수이다. 그러나 정규분포를 사용하여 비율 검정을 할 경우에 검정통계량 T를 연속형 확률변수로 가정하여 p-값 등이 계산된다. 이러한 이산형 확률변수와 연속형 확률변수 사이의 불일치를 해소하기 위하여 이산형 확률변수의 값 x를 마치 연속형 확률변수의 값인 것처럼 수정하게 되는데 이를 연속성 수정이라고 한다. 예를 들어 x=10이라는 이산형 값은 연속적인 수직선 상에서 [9.5, 10.5)의 구간을 의미하는 것으로 수정한다. prop.test()는 기본적으로 연속형 수정을 하여 가설검정을 수행한다. 연속형 수정을 하지 않고 가설점을 하려면 correct = FALSE로 인수를 설정한다. 다음은 Example 11.1을 연속형 수정을 하지 않고 정규분포로 비율 검정을 수행한 결과이다. 연속형 수정을 한 결과와 p-값이 조금 다른 것을 볼 수 있다.

> prop.test(20, 300, p = 0.1, alternative = "less", correct = FALSE)

    1-sample proportions test without continuity correction

data:  20 out of 300, null probability 0.1
X-squared = 3.7037, df = 1, p-value = 0.02715
alternative hypothesis: true p is less than 0.1
95 percent confidence interval:
 0.00000000 0.09443818
sample estimates:
         p 
0.06666667 

11.2 여러 모집단의 모비율의 차이에 대한 가설검정

11.2.1 prop.test()를 이용한 두 모집단의 모비율의 차이 검정

범주형 변수의 특정 범주에 대해 두 집단에서 모비율이 차이를 가설검정하는 방법을 살펴보자. 두 집단의 모비율의 차이를 검정하는 대표적인 예가 어떤 백신이 전염병에 효과가 있는지 없는지를 가설검정하는 것이다. 진짜 백신을 투여한 집단과 가짜 백신을 투여한 집단에서 전염병에 걸리는 비율에 차이가 있는지를 살펴보아 백신의 효과에 대해 가설검정을 수행한다. 이 때의 귀무가설은 백신은 효과가 없으므로 ’두 집단에서 전염병에 걸리는 비율은 같다’이고, 대립가설은 ’진짜 백신을 맞은 집단에서 전염병에 걸리는 비율이 가짜 백신을 맞은 집단보다 전염병에 걸리는 비율이 낮다’이다.

두 모집단의 모비율에 대해 가설검정을 하려면 두 집단에서 각각 \(n_1\)과 \(n_2\) 개의 표본을 추출하하여 관심있는 범주의 관측도수 \(x_1\)과 \(x_2\)를 측정한다. 그리고는 두 표본에서의 표본비율 \(\hat{p}_1\)과 \(\hat{p}_2\)을 다음과 같이 계산한다.

\[ \hat{p}_1 = x_1 / n_1, \quad \hat{p}_2 = x_2 / n_2. \]

두 집단의 모비율 차이에 대한 검정의 귀무가설은 ’두 모집단의 모비율 \(p_1\)과 \(p_2\)은 같다’로 수립하고, 대립가설은 모비율이 같지 않다, \(p_1\)이 더 크다, 작다로 수립한다. \(n_1\)과 \(n_2\)가 충분히 크면 두 집단의 모비율 차이의 검정통계량 \(T\)는 다음과 같이 정의될 수 있고 근사적으로 표준정규분포를 따른다.

\[ T = \frac{\hat{p}_1 - \hat{p}_2}{ \sqrt{ \hat{p} ( 1- \hat{p}) \left( \frac{1}{n_1} + \frac{1}{n_2} \right)}} \sim N(0, 1) \]

단, \(\hat{p} = (x_1 + x_2) / (n_1 + n_2)\).

대립가설에 따라 유의수준 \(\alpha\) 에 대해 기각역은 다음 표와 같다.

귀무가설 (\(H_0\))	대립가설 (\(H_1\))	기각역
\(p_1 = p_2\)	\(p_1 \neq p_2\)	\(T \ge z_{\alpha/2}\) 또는 \(T \le -z_{\alpha/2}\)
\(p_1 = p_2\)	\(p_1 < p_2\)	\(T \le -z_{\alpha}\)
\(p_1 = p_2\)	\(p_1 > p_2\)	\(T \ge z_{\alpha}\)

Example 11.4 기존 공정에서 400개를 생산했을 때 30개의 불량률이 발생하였다. 새로운 공정을 도입하고 300개의 제품을 생산한 후 불량품을 조사하였더니 20개가 발견되었다. 새로운 공정 도입으로 불량률이 저하되었는지 유의수준 5%에서 가설검정하시오.

Example 11.4은 새 공정의 불량률이 감소했다는 것을 검정하는 것이므로 기존 공정과 새 공정의 불량률을 \(p_1\)과 \(p_2\)라고 하면 귀무가설과 대립가설은 다음과 같다.

\[ \begin{align} H_0: & \quad p_1 = p_2 \\ H_1: & \quad p_1 > p_2 \end{align} \]

R의 prop.test() 함수는 두 모집단의 모비율의 차이 검정에도 사용된다.

prop.test(x = 관측도수_벡터, n = 표본수_벡터, alternative = "대립가설_종류")

prop.test() 함수를 여러 모집단의 모비율 차이를 검정할 때, 단일 모집단의 모비율 검정과의 차이는 다음과 같다.

• x와 n에 두 표본에서의 해당 범주의 관측도수와 표본 크기를 크기가 2인 벡터로 입력해야 한다. 이 때 주의해야 할 것은 x와 n 벡터에 두 집단의 정보를 나열할 때 귀무가설과 대립가설에서 첫 번째 모집단으로 설정된 표본의 값이 먼저 나열되어야 한다.
• 귀무가설이 두 모비율이 같다는 것이기 때문에, 단일 모집단에 대한 검정처럼 모비율을 특정 값으로 설정하지 않는다. 따라서 p 인수를 사용하지 않는다.

Example 11.4에서는 기존 공정을 첫 번째 모집단으로 신규 공정을 두 번째 모집단으로 설정하여 대립가설을 설정하였으므로, x와 n도 해당 순서로 데이터가 입력되었다. 대립가설은 \(p_1 > p_2\)이므로 "greater"로 설정되었다.

> prop.test(c(30, 20), c(400, 300), alternative = "greater")

    2-sample test for equality of proportions with continuity correction

data:  c(30, 20) out of c(400, 300)
X-squared = 0.075833, df = 1, p-value = 0.3915
alternative hypothesis: greater
95 percent confidence interval:
 -0.02668306  1.00000000
sample estimates:
    prop 1     prop 2 
0.07500000 0.06666667 

• 표본 비율 \(\hat{p}\)는 기존 공정과 신규 공정이 각각 0.075, 0.0666667이다.
• p-값은 0.3915127로 유의수준 0.05에서 귀무가설을 채택한다. (대립가설을 기각한다.)

따라서 신규 공정이 기존 공정보다 불량률이 낮다는 유의미한 통계적 증거는 없다고 할 수 있다.

11.2.2 교차표를 이용하여 여러 모집단의 모비율 차이를 검정하기

Example 11.5 course 데이터는 어떤 과목의 수강생에 대한 정보이다. 분반(class)에 따라 여학생 비율에 차이가 있었는지 유의수준 5%에서 가설검정하시오.

Example 11.5는 두 분반의 성별 차이가 있는지를 가설검정하는 것이다. 1분반과 2분반의 여학생 비율을 \(p_1\)과 \(p_2\)라고 하면 귀무가설과 대립가설은 다음과 같이 설정한다.

\[ \begin{align} H_0: & \quad p_1 = p_2 \\ H_1: & \quad p_1 \neq p_2 \end{align} \] prop.test() 함수의 x와 n 인수에 입력할 데이터를 구하려면 분반-성별 교차표를 계산하여야 한다.

> tcg <- xtabs(~ class + gender, data = course)
> tcg

     gender
class  F  M
    1 10 12
    2  8 15

x는 분반별 여학생의 수이므로 tcg의 첫번째 열이고, n은 분반별 학생 수이므로 tcg의 행별 합이된다. 그러므로 다음처럼 prop.test() 함수를 이용하여 두 분반의 여학생 비율의 차이에 대한 가설검정을 수행할 수 있다.

> prop.test(tcg[,1], marginSums(tcg, 1), alternative = "two.sided")

    2-sample test for equality of proportions with continuity correction

data:  tcg[, 1] out of marginSums(tcg, 1)
X-squared = 0.18157, df = 1, p-value = 0.67
alternative hypothesis: two.sided
95 percent confidence interval:
 -0.2226672  0.4361059
sample estimates:
   prop 1    prop 2 
0.4545455 0.3478261 

• 여학생의 표본 비율 \(\hat{p}\)는 1, 2 분반이 각각 0.4545455, 0.3478261이다.
• p-값은 0.6700265로 유의수준 0.05에서 귀무가설을 채택한다. (대립가설을 기각한다.)

따라서 분반별 성별 비율의 차이에 대한 통계적 증거는 없다고 할 수 있다.

교차표를 직접 인수로 전달하여 가설검정하기

그런데 모비율의 차이에 대한 가설검정을 하기 위하여 교차표에서 매번 열을 지정하여 x에 전달하고, 행별 합을 구하여 n에 전달하는 작업은 조금 번거로운 작업이다. prop.test()는 교차표를 첫 번째 인수로 직접 전달받아 모비율의 차이에 대한 가설검정을 수행할 수 있다. 이 때 첫 번째 인수로 전달될 교차표는 다음 조건이 만족되어야 한다.

• 교차표의 행은 모집단을 표현한다. Example 11.5에서 모집단은 분반이 된다.
• 교차표의 열은 검정하려는 범주형 변수를 표현해야 한다. Example 11.5에서 검정하고자 하는 범주형 변수는 성별이다.
• 교차표는 두 열만을 가져야 한다. 즉, 검정하고자 하는 범주형 변수의 범주는 두 개이어야 한다. Example 11.5의 범주형 변수는 성별이고 여자(F)와 남자(M)라는 두 변수만 가지고 있다.
• 모비율을 계산할 때 교차표의 첫 번째 열을 기준으로 계산을 수행한다. 그러므로 교차표 tcg에서는 여자의 비율을 계산하여 가설검정한다. 사실 두 개의 범주만 있는 경우에는 두 범주 중 무엇을 기준으로 계산하는 지는 표본비율에만 영향을 미치지 가설검정의 결과에는 영향을 미치지는 않는다.

따라서 모비율 가설검정을 할 때 xtabs()을 이용하여 교차표를 만들 때 다음처럼 교차표를 만들어 가설검정을 수행하면 된다.

교차표_결과 <- xtabs(~ 모집단_구분_변수 + 검정할_범주형_변수, data = 데이터)
prop.test(교차표_결과, alternative = "대립가설_종류")

x와 n 인수에 직접 값을 입력한 결과와 동일한 결과를 주는 것을 확인할 수 있다.

Example 11.5은 분반을 각각의 모집단으로 하여 성별 비율의 차이를 검정하는 것이므로 분반이 행, 성별이 열이 되도록 교차표를 만들었다. 그리고 prop.test()는 모집단의 그룹을 행으로, 검정하려는 범주형 변수를 열로 된 교차표를 직접 입력 받아 가설검정을 수행하였다.

> tcg

     gender
class  F  M
    1 10 12
    2  8 15

> prop.test(tcg, alternative = "two.sided")

    2-sample test for equality of proportions with continuity correction

data:  tcg
X-squared = 0.18157, df = 1, p-value = 0.67
alternative hypothesis: two.sided
95 percent confidence interval:
 -0.2226672  0.4361059
sample estimates:
   prop 1    prop 2 
0.4545455 0.3478261 

만약 Example 11.5 범주형 변수의 순서를 변경하여 남자(M)가 첫 번째 열에 나오도록 하여 남자의 모비율을 가지고 가설검정을 하려면 어떻게 해야 할까? factor() 함수를 사용하여 범주형 변수의 범주(levels)의 순서를 바꾼 후 교차표를 만들면 된다.⁸ (factor()에 대한 자세한 내용은 R 프로그래밍의 범주형 데이터와 요인 절을 참조하기 바란다.) 다음은 남자와 여자의 순서를 바꾸어 교차표를 만든 후 앞의 가설 검정을 다시 수행한 결과이다. p-값 등이 모두 동일하고 단지 여자가 아니라 남자로 표본비율을 계산하였기 때문에 모비율의 추정 값이 달라지는 것을 볼 수 있다.

> tcgM <- xtabs(~ class + factor(gender, levels=c("M", "F")), data = course)
> tcgM

     factor(gender, levels = c("M", "F"))
class  M  F
    1 12 10
    2 15  8

> prop.test(tcgM, alternative = "two.sided")

    2-sample test for equality of proportions with continuity correction

data:  tcgM
X-squared = 0.18157, df = 1, p-value = 0.67
alternative hypothesis: two.sided
95 percent confidence interval:
 -0.4361059  0.2226672
sample estimates:
   prop 1    prop 2 
0.5454545 0.6521739 

사례 연구: 여러 모집단의 모비율 차이에 대한 가설검정

Example 11.6 bizstatp 패키지의 BrokenMarriage는 덴마크 사회 조사국에서 수행한 성별 및 사회적 계급에 따라 이혼 또는 영구적 관계가 깨진 빈도를 측정한 데이터이다. 여성의 경우 사회적 등급(rank)에 따라 이혼 비율이 다른지 유의수준 5% 하에 가설검정 하시오.

> BrokenMarriage

   Freq gender rank broken
1    14   male    I    yes
2   102   male    I     no
3    39   male   II    yes
4   151   male   II     no
5    42   male  III    yes
6   292   male  III     no
7    79   male   IV    yes
8   293   male   IV     no
9    66   male    V    yes
10  261   male    V     no
11   12 female    I    yes
12   25 female    I     no
13   23 female   II    yes
14   79 female   II     no
15   37 female  III    yes
16  151 female  III     no
17  102 female   IV    yes
18  557 female   IV     no
19   58 female    V    yes
20  321 female    V     no

Example 11.6은 다섯 개의 사회적 계급별로 여성의 이혼율이 같은지를 가설검정하는 것으로 \(p_i\)를 등급 \(i\)의 여성의 이혼율이라고 하면 귀무가설과 대립가설은 다음과 같다. 두 모집단의 경우 대립가설이 모비율이 같지 않다, 작다, 크다의 세 종류가 있지만 모집단이 3 개 이상이 되면 모비율이 서로 같지 않은 두 집단이 있다라는 한 가지 종류밖에 없다.

\[ \begin{align} H_0: & \quad p_1 = p_2 = \cdots = p_5 \\ H_1: & \quad p_i \neq p_j \text{인 } i, j \text{가 있다. 단, } i, j = 1, 2, \ldots, 5, i \neq j. \end{align} \] prop.test()에 교차표를 전달하여 가설검정을 하려면 교차표의 행이 모집단을 표현하고, 열이 검정하려는 범주형 변수를 표현해야 한다. Example 11.6는 사회적 계급을 행으로, 이혼 여부를 열로 교차표를 만들면 된다. BrokenMarriage는 이미 범주별로 관측도수가 요약된 데이터이다. 이렇게 이미 요약된 데이터를 이용하여 빈도표를 만드는 방법은 7.3.2 절에서 설명한 것처럼 xtabs() 함수의 수식 좌변에 관측도수를 나타내는 열을 지정하는 것이다. 아울러 여자의 이혼률에 대해서만 가설검정하려는 것이므로, subset 인수를 사용하여 성별이 여자인 데이터로 한정하여 교차표를 만들도록 하였다.

> trb_femail <- xtabs(Freq ~ rank + broken, data = BrokenMarriage, 
+                     subset = gender == "female")
> trb_femail

     broken
rank  yes  no
  I    12  25
  II   23  79
  III  37 151
  IV  102 557
  V    58 321

prop.test()를 이용하여 가설검정을 하면 다음과 같은 결과를 얻는다. 이 때 모집단이 3 개 이상이면 모비율이 서로 같지 않은 두 집단이 있다라는 한 종류의 대립가설만 있으므로 alternative 인수는 기술하지 않는다.

> prop.test(trb_femail)

    5-sample test for equality of proportions without continuity correction

data:  trb_femail
X-squared = 11.286, df = 4, p-value = 0.02353
alternative hypothesis: two.sided
sample estimates:
   prop 1    prop 2    prop 3    prop 4    prop 5 
0.3243243 0.2254902 0.1968085 0.1547800 0.1530343 

• 표본 비율 \(\hat{p}\)은 사회적 계급 별로 각각 0.3243243, 0.2254902, 0.1968085, 0.15478, 0.1530343이다.
• p-값은 0.023535로 유의수준 0.05에서 귀무가설을 기각한다. (대립가설을 채택한다.)

따라서 여성의 사회적 계급 별로 이혼율의 차이가 있다고 할 수 있다. 모집단이 세 개 이상인 경우의 모비율의 차이에 대한 가설검정에서 귀무가설이 기각되고 대립가설이 채택되면, 어느 모집단이 전체 데이터의 평균 비율보다 유의미하게 컸는지 작았는지에 대한 분석이 필요하다. 이를 분석하는 방법에 대해서는 카이제곱 검정을 사용하는 독립성 검정에서 논의하도록 한다. 사실 prop.test()도 모비율의 차이에 대한 가설검정을 카이제곱 검정으로 하기 때문에 다음처럼 chisq.test()를 사용해도 동일한 결과를 얻는다. 다만 chisq.test()는 이 검정이 모집단의 모비율에 대한 가설 검정인지 분포에 대한 독립성 검정인지 구분하지 못하므로 표본 비율에 대한 정보는 제공하지 않는다.

> chisq.test(trb_femail)

    Pearson's Chi-squared test

data:  trb_femail
X-squared = 11.286, df = 4, p-value = 0.02353

11.2.3 Fisher의 Exact Test

Example 11.7 course 데이터는 어떤 과목의 수강생에 대한 정보이다. 학년(year)에 따라 여학생 비율에 차이가 있었는지 유의수준 5%에서 가설검정하시오.

Example 11.7은 학년간 성별 차이가 있는지를 가설검정하는 것으로 각 학년의 여학생 비율을 \(p_i\)라고 하면 귀무가설과 대립가설은 다음과 같다.

\[ \begin{align} H_0: & \quad p_1 = p_2 = p_3 = p_4 \\ H_1: & \quad p_i \neq p_j \text{인 } i, j \text{가 있다. 단, } i, j = 1, 2, 3, 4, i \neq j. \end{align} \]

Example 11.7은 학년을 각각의 모집단으로 하여 성별 비율의 차이를 검정하는 것이므로 학년이 행, 성별이 열이 되도록 교차표를 만든다.

> tyg <- xtabs(~ year + gender, data = course)
> tyg

    gender
year  F  M
   1  0  1
   2 14 18
   3  3  6
   4  1  2

앞에서 구해진 교차표를 prop.test()고 전달하여 가설검정을 하면 다음 결과를 얻는다.

> prop.test(tyg)

Warning in prop.test(tyg): Chi-squared approximation may be incorrect

    4-sample test for equality of proportions without continuity correction

data:  tyg
X-squared = 1.0764, df = 3, p-value = 0.7828
alternative hypothesis: two.sided
sample estimates:
   prop 1    prop 2    prop 3    prop 4 
0.0000000 0.4375000 0.3333333 0.3333333 

그런데 가설검정을 해보면 결과가 정확하지 않을 수 있다는 경고가 나타난다. 여러 모집단의 모비율에 대한 가설검정은 Peason의 카이제곱 검정을 하는데 이 검정 방법은 범주형 변수를 연속형 변수로 근사하여 수행하게 된다. 그리고 한 셀의 관측도수의 기대치가 최소 5 이상이어야만 이러한 근사가 어느 정도 정확할 수 있다. 그런데 Example 11.7은 2학년을 제외하고는 다른 셀의 관측도수가 적어서 기대치가 5 미만인 셀이 많다.

이렇듯 교차표의 셀의 관측치가 적은 경우에는 Fisher의 Exact Test를 수행하는 것이 좋다. 단일 모집단의 모비율에 대해 검정할 때 이항분포를 사용하여 정확한 분포로 가설섬정을 할 수 있었던 것과 마찬가지로, Fisher의 Exact Test는 초기하 분포라는 이산형 분포를 사용하여 정확한 가설검정을 수행할 수 있다.

R에서 Fisher의 Exact Test를 하는 함수fisher.test() 함수이다. prop.test() 함수와 마찬가지로

> fisher.test(tyg)

    Fisher's Exact Test for Count Data

data:  tyg
p-value = 0.9235
alternative hypothesis: two.sided

prop.test()와 달리 표본 비율에 대한 정보는 주지 않는다. p-값은 0.9234755로 유의수준 0.05에서 귀무가설을 채택한다. (대립가설을 기각한다.) 그러므로 학년별로 성별 비율에 차이가 있었다는 통계적 증거는 없었다.

11.3 적합성 검정

지금까지는 범주형 변수에서 한 범주가 발생하는 비율에 대한 가설검정을 살펴보았다. 성별 변수에서 여학생의 비율, 학년 변수에서 2학년의 비율 등이 그 예라 할 수 있다. 이제부터는 범주형 변수에서 한 범주의 비율이 아니라 전체 범주의 분포에 대하여 가설검정하는 방법을 살펴보자. 즉, 학년 변수에서 특정 학년의 비율이 아니라 전체 학년의 분포에 대해 가설검정을 하는 것이 그 예라 할 수 있다.

적합성 검정(Goodness-of-Fit Test)은 \(k\) 개의 범주를 가지는 범주형 변수에 대하여 모집단에서 각 범주의 발생 비율이 특정 값인지 아닌지를 검정한다. 범주형 변수의 \(i\)-번째 범주의 모집단에서의 비율을 \(p_i\)라고 하자. 단, \(i=1, \ldots, k\). \(\sum_{i} p_i = 1\). 그러면 적합성 검정에서의 귀무가설은 다음과 같다.

\[ H_0: \quad p_1 = p_{10}, \, p_2 = p_{20}, \, \ldots, \, p_k = p_{k0} \]

대립가설 \(H_1\)은 ’위의 조건 중 하나 이상이 만족하지 않는다’가 된다.

모집단에서 \(n\)개의 표본을 임의로 추출하였을 때, \(i\)-번째 범주의 관측치의 수를 나타내는 확률변수를 \(X_i\)라고 하자. 그러면 \(\sum_{i=1}^{k} X_i = n\)이고, 귀무가설이 맞다면 표본 분포는 다음과 같은 다항분포를 따른다.

\[ (X_1, X_2, ..., X_k) \sim \text{multinomial}(n, p_{10}, p_{20}, .... p_{k0}) \]

표본의 크기가 \(n\)일 때 범주 별 관측도수 \((X_1, X_2, ..., X_k)\)가 다항분포를 따르면, 다음처럼 정의되는 검정통계량 \(X^2\)는 자유도 \((k-1)\)의 카이제곱 분포로 근사적으로 따른다고 알려져 있다.

\[ X^2 = \sum_{i=1}^{k} \frac{[X_i-E(X_i)]^2}{E(X_i)} = \sum_{i=1}^{k} \frac{[X_i- n \, p_{i0}]^2}{n \, p_{i0}}. \] 즉,

\[ X^2 \sim \chi^2(k-1). \]

그런데 이러한 근사 방법이 잘 작동하려면 각 범주의 기대 관측도수 \(E(X_i) = n p_i\)가 5 이상이어야 한다. 이보다 작으면 근사의 정확도가 떨어진다.

귀무가설이 맞는다면 표본의 각 범주의 실제 관측도수 \(x_i\)가 기대치 \(n \, p_i\)와 가까워지고, 그렇지 않으면 차이가 나게 된다. 따라서 귀무가설의 조건이 성립하지 않으면 \(X^2\) 값이 커지게 된다. 따라서 적합성 검정은 카이제곱 분포를 이용하여 오른쪽 단측검정으로 가설검정을 수행한다.

Example 11.8 3가지 색상으로 구성된 제품이 판매되고 있다. 고객이 특별히 선호하는 색상은 없고 동일한 비율로 판매된다는 가설에 대해 검정하고자 한다. 시험적으로 판매된 \(n=90\)개 판매 데이터를 분석해 보니, 각 색상별 판매량이 \(x_1 = 23, x_2 = 36, x_3 = 31\)로 집계되었다. 유의수준 5%에서 가설검정을 하시오.

세가지 색상의 고객 선호 비율을 각각 \(p_1, p_2, p_3\)라고 하면 귀무가설과 대립가설은 다음과 같다.

\[ \begin{align} H_0: \quad & p_1 = p_2 = p_3 = 1/3\\ H_1: \quad & p_i \neq 1/3 \, \text{ for some } \, i. \end{align} \]

R에서는 chisq.test() 함수를 이용하면 적합성 검정을 한다.

chisq.test(x = 범주별_관측도수, p = 범주별_비율)
chisq.test(x = 범주별_관측도수, p = 범주별_비율, rescale.p, correct)

• x: 각 범주별 관측치 수를 나타내는 벡터 또는 빈도표
• p: 적합성 검정을 할 때 사용할 귀무가설 하의 범주별 비율을 나타내는 벡터
• rescale.p: p의 합이 1이 아닐 때, 1이 되도록 스케일을 조정할지를 결정하는 논리값 인수
• correct: 연속성 수정을 할지를 결정하는 논리값 인수

이 외에도 카이제곱 확률분포를 사용한 가설검정이 아니라 몬테 카를로 시뮬레이션을 이용한 가설검정을 할 때 사용하는 simulation.p.value와 B 인수가 있다. 이에 대해서는 뒤에 설명을 하겠다.

다음은 Example 11.8의 카이제곱 검정 결과이다. 기본적으로 출력되는 정보뿐 아니라 상세 정보를 이용하기 위해 결과를 변수에 할당한 후 출력하였다.

> result <- chisq.test(c(23, 36, 31), p=c(1/3, 1/3, 1/3))
> result

    Chi-squared test for given probabilities

data:  c(23, 36, 31)
X-squared = 2.8667, df = 2, p-value = 0.2385

위의 예에서는 p-value가 0.2385126가 나와 유의수준 0.05에서 귀무가설을 채택한다. (대립가설을 기각한다.)

chisq.test()를 수행한 결과를 변수에 저장하면 화면에 출력되지 않은 상세한 정보를 나중에 확인할 수 있다. 어떠한 상세 정보를 제공하는지 확인하려면 names() 함수를 이용하여 변수에 저장된 요소의 이름을 출력해 본다.

> names(result)

[1] "statistic" "parameter" "p.value"   "method"    "data.name" "observed" 
[7] "expected"  "residuals" "stdres"   

chisq.test()의 결과 중에서 중요한 요소가 observed, expected, residuals, stdres이다.

• observed는 각 범주별 관측 개수이다.
• expected 는 귀무가설 하에서 각 범주별 관측 개수의 기대치이다.
• residuals은 \([x_i-E(x_i)]/\sqrt{E(x_i)}\)의 값이다. 따라서 residual을 제곱하여 다 더하면 \(X^2\)가 된다.
• stdres는 표준화된 잔차로 \([x_i-E(x_i) ]/SE( x_i-E(x_i) )\)로 셀의 관측값이 커지면 정규분포에 근사된다.

chisq.test()의 결과의 각 요소를 출력하려면, 출력결과$요소의 명령을 사용하면 된다.

> result$observed

[1] 23 36 31

> result$expected

[1] 30 30 30

> result$residuals

[1] -1.2780193  1.0954451  0.1825742

> result$stdres

[1] -1.5652476  1.3416408  0.2236068

stdres를 살펴보면 귀무가설을 기각하게 만드는데 기여한 셀이 무엇인지 확인할 수 있다.

• 일반적으로 한 범주의 stdres의 절대값이 2보다 크면 그 셀의 관측치가 귀무가설 하의 기대치에서 크게 차이가 난 것으로, 3이상이면 차이가 매우 크게 난 것으로 판단한다.
• stdres 값이 양수이면 관측치가 귀무가설 하의 기대치에 비해 컸다는 것이며, 음수이면 관측치가 귀무가설 하의 기대치보다 작았다는 것이다.
• 여기서 주의할 점은 귀무가설이 맞더라도 표준화된 잔차의 절대값이 2이상일 확률은 정규분포 하에서 약 5%가 된다. 따라서 20개의 범주가 있다면 귀무가설이 맞더라도 표준화된 잔차의 절대값이 2 이상이 되는 셀이 평균적으로 1개 정도는 나타나게 된다. 따라서 귀무가설의 채택과 기각 여부는 p-값으로 판단해야지 stdres로 판단해서는 안된다.

Example 11.8의 예에서는 귀무가설을 기각하지 못했고 모든 범주에 대해 stdres의 값이 \(\pm 2\) 구간 안에 있으므로 각 범주별 표본의 관측 개수가 기대치를 크게 벗어나지 않았다.

Example 11.9 어느 지역에서 발생하는 하루 동안의 교통사고 수 \(Y\)를 \(n=50\)일간 조사하였다. 조사한 결과 다음과 같은 결과를 얻었다. 교통사고 수 \(Y\)가 \(\lambda = 1/2\)인 포아송 분포를 따르는지에 대해서 유의수준 5%에서 가설검정 하시오.

y	frequency
0	32
1	12
2 이상	6

귀무가설과 대립가설은 다음과 같다. \[ \begin{align} H_0: \quad & Y \sim Poisson(1/2) \\ H_1: \quad & Y \text{는 Poisson(1/2) 분포를 따르지 않는다.} \end{align} \]

귀무가설 하의 사고가 하루에 0번, 1번, 2번 이상 일어날 확률을 다음처럼 \(p_1, p_2, p_3\)라고 하자.

\[p_1 = P(Y=0), \, p_2=P(Y=1), \, p_3 = P(Y \ge 2).\] 그러면 귀무가설 하의 \(p_1, p_2, p_3\)는 다음처럼 포아송 분포의 확률질량함수를 이용하여 구할 수 있다.

> lambda <- 1/2
> p <- c(dpois(c(0, 1), lambda), ppois(1, lambda, lower.tail=F)); p

[1] 0.60653066 0.30326533 0.09020401

chisq.test() 함수로 가설검정을 수행하면 다음 결과를 얻는다.

> result <- chisq.test(c(32, 12, 6), p=p); result

Warning in chisq.test(c(32, 12, 6), p = p): Chi-squared approximation may be
incorrect

    Chi-squared test for given probabilities

data:  c(32, 12, 6)
X-squared = 1.2444, df = 2, p-value = 0.5368

위의 예에서는 p-value가 0.5367749가 나와 유의수준 0.05에서 귀무가설을 채택한다. (대립가설을 기각한다.) 그러므로 교통사고가 포아송 분포가 아니라는 통계적 증거는 없었다.

그러나 마지막 셀의 기대치가 5 미만이어서 가설검정에 정확성에 대한 경고가 출력되었다.

> result$expected

[1] 30.326533 15.163266  4.510201

만약 \(\lambda\)가 주어져 있지 않으면, 최우추정법(Maximum Likelihood Estimate)를 이용하여 \(\lambda\)를 추정해야 하고, 이 경우 \(\chi^2\) 분포의 자유도가 1 감소하게 된다. 이러한 경우에도 R을 사용하여 가설검정을 수행할 수 있는데, 이에 대한 설명은 이 교재의 범위를 넘어가므로 설명을 생략하도록 한다.

11.3.1 빈도표를 이용한 적합성 검정

Example 11.10 course 데이터는 어떤 과목의 수강생에 대한 정보이다. 학년(year)별 수강 신청 비율이 0.05, 0.6, 0.25, 0.1이라는 귀무가설에 대하여 유의수준 5%에서 가설검정하시오.

Example 11.10에서 각 학년의 수강생 비율을 \(p_i\)라고 하면 귀무가설은 다음과 같다.

\[ H_0: \quad p_1 = 0.05, \, p_2 = 0.6, \, p_3 = 0.25, \, p_4 = 0.1 \]

학년별 수강생의 절대 빈도표와 상대 빈도표를 구하면 다음과 같다.

> ty <- xtabs(~ year, data = course)
> ty

year
 1  2  3  4 
 1 32  9  3 

> proportions(ty)

year
         1          2          3          4 
0.02222222 0.71111111 0.20000000 0.06666667 

chisq.test()로 가설검정을 하면 다음의 결과를 얻는다.

> result <- chisq.test(ty, p = c(0.05, 0.6, 0.25, 0.1))

Warning in chisq.test(ty, p = c(0.05, 0.6, 0.25, 0.1)): Chi-squared
approximation may be incorrect

> result

    Chi-squared test for given probabilities

data:  ty
X-squared = 2.5704, df = 3, p-value = 0.4627

> result$expected

    1     2     3     4 
 2.25 27.00 11.25  4.50 

그러나 1학년과 4학년의 기대 관측도수가 5보다 작아서 가설검정의 정확성에 대한 경고가 출력되었다.

11.3.2 몬테 카를로 시뮬레이션을 이용한 적합도 가설검정

Example 11.10는 기대 관측도수가 5보다 작은 범주가 있으므로 카이제곱 검정의 정확도가 떨어진다. 단일모집단의 모비율 검정에서 이항분포를 사용하면 정확한 검정을 할 수 있는 것과 마찬가지로 적합도 검정을 원래의 정확한 분포인 다항분포를 사용하여 수행하면 기대 관측도수가 작더라도 정확한 가설검정을 수행할 수 있다. 그러나 다항분포를 이용하여 p-값을 계산하는 것은 매우 강도 높은 계산량을 요구한다. 그래서 다항분포의 식을 이용하여 p-값을 직접 구하기보다는 몬테 카를로 시뮬레이션을 이용하여 p-값을 구한다.

\(n\)개의 표본을 임의로 추출하였을 때 귀무가설 하에 범주의 관측도수 \((x_1, x_2, \dots, x_k)\)는 다항분포 \(\text{multinomial}(n, p_{10}, p_{20}, .... p_{k0})\)를 따른다. 몬테 카를로 시뮬레이션은 다항분포를 따르는 관측도수 \((x_1, x_2, \dots, x_k)\)를 B 번 시뮬레이션을 구한다. 그리고 이 B 번의 시뮬레이션 값 중에서 현재 관측된 관측도수보다 더 예외적인 결과가 나온 시뮬레이션 횟수를 구하여 p-값을 추정한다. 예를 들어 \(B=1000\)번 시뮬레이션 했는데, 이 중 25 번의 결과가 현재 관측된 값보다 더 예외적인 값이라면 현재 관측된 값보다 예외적인 값이 나올 확률은 \(25 / 1000 = 2.5\) %라고 추정한다.

chisq.test() 함수가 근사적인 카이제곱 분포가 아니라 다항분포를 몬테 카를로 시뮬레이션 하여 p-값을 구하게 하려면 simulate.p.value = TRUE로 설정하면 된다. 시뮬레이션 횟수는 2,000번으로 설정되어 있다. 인수 B를 설정하면 시뮬레이션 횟수를 조정할 수 있다.

> result <- chisq.test(ty, p = c(0.05, 0.6, 0.25, 0.1), 
+                      simulate.p.value = TRUE)
> result

    Chi-squared test for given probabilities with simulated p-value (based
    on 2000 replicates)

data:  ty
X-squared = 2.5704, df = NA, p-value = 0.4723

위의 예에서는 p-value가 0.4722639가 나와 유의수준 0.05에서 귀무가설을 채택한다. (대립가설을 기각한다.) 앞에서 근사적으로 카이제곱 분포로 p-값을 구한 결과와 큰 차이를 보이지는 않았다.

11.4 독립성 검정

독립성 검정은 어떤 두 범주형 변수가 독립인지 아닌지를 검정한다. 첫 번째 범주형 변수에 \(R\)개의 범주가 있고, 두 번째 범주형 변수에 \(C\)개의 범주가 있다고 하자. 그러면 두 범주형 변수와 관련된 교차표 또는 분할표는 \(R \times C\) 행렬로 표현된다.

범주	1	2	\(\cdots\)	C	합계
1	\(x_{11}\)	\(x_{12}\)	\(\cdots\)	\(x_{1C}\)	\(r_1\)
2	\(x_{21}\)	\(x_{22}\)	\(\cdots\)	\(x_{2C}\)	\(r_2\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\ddots\)	\(\vdots\)	\(\vdots\)
R	\(x_{R1}\)	\(x_{R2}\)	\(\cdots\)	\(x_{RC}\)	\(r_R\)
합계	\(c_{1}\)	\(c_{2}\)	\(\cdots\)	\(c_{C}\)	\(n\)

\(n\)을 전체 관측도수, \(x_{ij}\)를 i행-j열 셀의 관측도수라고 하자. 그리고 \(r_i\)와 \(c_j\)를 각각 i 행과 j 열의 관측도수의 합이라고 하자. 그러면 독립성 검정의 검정통계량 \(X^2\)은 다음과 같다.

\[ X^2 = \sum_{i=1}^{R} \sum_{j=1}^{C} \frac{[x_{ij} - E(x_{ij})]^2}{E(x_{ij})} = \sum_{i=1}^{R} \sum_{j=1}^{C} \frac{[(x_{ij} - r_i \, c_j / n)]^2}{r_i \, c_j / n} \]

그리고 검정통계량 \(X^2\)는 자유도 \((R-1) (C-1)\)의 카이제곱 분포를 따른다.

\[ X^2 \sim \chi^2((R-1)(C-1)). \]

적합성 검정과 마찬가지로 두 변수의 독립성 가정이 참이면 각 셀의 관측도수 \(x_{ij}\)와 귀무가설 하의 각 셀의 기대관측치 \(r_i \, c_j / n\)의 차이가 크지 않고, 거짓이면 차이가 커지게 된다. 따라서 독립성 검정도 \(X^2\)이 예외적으로 커지면 대립가설을 받아들이므로 오른쪽 단측검정을 한다.

Example 11.6에서는 사회 계급에 따라 여성의 이혼 비율에 대해 가설검정한 것이지만, 여성의 사회적 계급(rank)과 이혼 여부(broken)라는 두 변수의 독립성을 검정하는 문제로 보고 카이제곱 검정을 수행할 수도 있다.

> trb_femail

     broken
rank  yes  no
  I    12  25
  II   23  79
  III  37 151
  IV  102 557
  V    58 321

> result <- chisq.test(trb_femail)
> result

    Pearson's Chi-squared test

data:  trb_femail
X-squared = 11.286, df = 4, p-value = 0.02353

그런데 앞서서 p-값이 0.023535로 유의수준 0.05보다 작으므로 귀무가설이 기각된다고만 하고, 귀무가설이 기각된 이유에 대한 분석을 하지 않았다. 제대로 된 분석을 하려면 귀무가설이 기각되는 경우 어떠한 요인이 귀무가설을 기각하게 만들었는지를 살펴보아야 한다. 적합성 검정과 마찬가지로 stdres은 귀무가설이 맞다고 할 때 각 셀의 실제 관측도수가 기대 관측도수에서 얼마나 크게 벗어났는지를 알려준다.

> result$stdres

     broken
rank        yes        no
  I    2.534424 -2.534424
  II   1.552177 -1.552177
  III  1.055350 -1.055350
  IV  -1.442944  1.442944
  V   -1.032415  1.032415

결과에서 보듯이 사회 계급 별로 이혼 여부의 차이를 만든 두드러진 요인은 사회 계급이 1등급인 여성이 전체 평균에 비해 이혼한 경우(yes)는 더 많고 이혼 하지 않은 경우(no)는 더 적었기 때문이었다. 그 다음으로 전체적인 이혼 추세에서 벗어난 계급은 2등급 여성과 4등급 여성이었다. 2등급은 1등급만큼은 아니지만 이혼 비율이 평균적인 이혼 비율보다 높았고, 4등급은 이혼 비율이 평균보다 낮았다.

Example 11.11 bizstatp에 포함된 Arthritis 데이터에서 치료의 종류(Treatment)와 증상 개선 효과(Improved)가 서로 독립인지 유의수준 5% 하에 가설검정하시오.

Arthritis 데이터에서 치료의 종류와 개선 효과에 대해 교차표를 구하면 다음과 같다.

> tti <- xtabs(~ Treatment + Improved, data = Arthritis)
> tti

         Improved
Treatment None Some Marked
  Placebo   29    7      7
  Treated   13    7     21

chisq.test() 함수를 이용하여 독립성 검정을 하면 다음과 같은 결과를 얻는다.

> result <- chisq.test(tti)
> result

    Pearson's Chi-squared test

data:  tti
X-squared = 13.055, df = 2, p-value = 0.001463

위의 예에서는 p-value가 0.0014626가 나와 유의수준 0.05에서 귀무가설을 기각한다. (대립가설을 채택한다.) 즉, 치료법이 플라시보인지 진짜 치료인지에 따라 증상 개선에 차이가 있었다.

그러면 귀무가설을 기각시킨 주요 요인이 무엇인지 확인해 보자. 아래 결과를 보면, 플라시보 치료군에서는 귀무가설이 맞다고 할 때 기대되는 관측도수에 비해 증상 개선 없음(None)이 훨씬 많았고, 증상의 확실한 개선(Marked)은 훨씬 적었다. 반면 진짜 치료는 귀무가설이 맞다고 할 때 기대되는 관측도수에 비해 증상 개선 없음(None)이 훨씬 적었고, 증상의 확실한 개선(Marked)은 훨씬 많았다.

> result$stdres

         Improved
Treatment        None        Some      Marked
  Placebo  3.27419655 -0.09761768 -3.39563632
  Treated -3.27419655  0.09761768  3.39563632

Example 11.12 course 데이터는 어떤 과목의 수강생에 대한 정보이다. 학년(year) 분포와 분반(class)의 분포는 서로 독립이라는 귀무가설에 대하여 유의수준 5%에서 가설검정하시오.

교차표와 카이제곱 검정을 이용하여 가설검정을 하면 다음 결과를 얻는다.

> tcy <- xtabs(~ class + year, data = course)
> tcy

     year
class  1  2  3  4
    1  0 18  3  1
    2  1 14  6  2

> result <- chisq.test(tcy)

Warning in chisq.test(tcy): Chi-squared approximation may be incorrect

> result

    Pearson's Chi-squared test

data:  tcy
X-squared = 2.8125, df = 3, p-value = 0.4214

> result$expected

     year
class         1        2   3        4
    1 0.4888889 15.64444 4.4 1.466667
    2 0.5111111 16.35556 4.6 1.533333

2학년을 제외한 모든 셀의 기대 관측도수가 5 이하여서 카이제곱 분포를 사용한 가설검정이 적절하지 않기 때문에 경고 메시지가 출력되었다. 독립성 검정에서 셀의 기대 관측도수가 5 이하여서 경고가 나오는 경우에는 fisher.test() 함수를 이용하여 독립성에 대하여 Fisher의 Exact Test를 수행하는 것이 좋다.

> fisher.test(tcy)

    Fisher's Exact Test for Count Data

data:  tcy
p-value = 0.4427
alternative hypothesis: two.sided

그런데 fisher.test()도 셀이 너무 많아지면 p-값 계산 시간이 많이 소요된다. 이러한 경우는 chisq.test()와 마찬가지 방식으로 몬테 카를로 시뮬레이션으로 p-값을 계산할 수 있다. Example 11.12는 그러한 경우는 아니지만 예제 삼아 몬테 카를로 시뮬레이션을 이용하여 p-값을 구해보자. 정확한 분포로 구한 결과와 시뮬레이션 결과에 큰 차이가 없음을 볼 수 있다.

> fisher.test(tcy, simulate.p.value = TRUE)

    Fisher's Exact Test for Count Data with simulated p-value (based on
    2000 replicates)

data:  tcy
p-value = 0.4443
alternative hypothesis: two.sided

몬테 카틀로 시뮬레이션으로 독립성 검정을 하려면 chisq.test() 함수를 사용하여도 된다. 두 함수 모두 동일한 방식으로 시뮬레이션을 하여 p-값을 구한다. 다만 시뮬레이션 결과가 매번 다르므로 p-값은 실행할 때마다 다를 수 있다. 다음은 동일한 시뮬레이션 값이 나오도록 시드를 동일하게 한 후 두 함수의 결과를 비교한 것이다. 시뮬레이션 결과가 동일하면 p-값이 동일함을 확인할 수 있다.

> set.seed(12)
> chisq.test(tcy, simulate.p.value = TRUE)

    Pearson's Chi-squared test with simulated p-value (based on 2000
    replicates)

data:  tcy
X-squared = 2.8125, df = NA, p-value = 0.4598

> set.seed(12)
> fisher.test(tcy, simulate.p.value = TRUE)

    Fisher's Exact Test for Count Data with simulated p-value (based on
    2000 replicates)

data:  tcy
p-value = 0.4598
alternative hypothesis: two.sided

11.5 범주형 변수의 가설검정에 대한 정리

그림 11.1은 지금까지 살펴본 범주형 변수에 대한 여러 가지 가설검정의 차이점을 도식화하여 분류한 것이다. 범주형 변수의 가설검정은 크게 범주 하나의 비율에 대한 것인지 아니면 모든 범주에 대한 분포에 대한 것인지에 따라 나뉘어진다. 그리고 한 범주의 비율에 대한 검정은 하나의 모집단에서의 모비율에 대한 검정인지, 여러 모집단의 모비율의 차이에 대한 것인지에 따라 다시 나뉘어진다. 분포 검정도 마찬가지로 하나의 범주형 변수의 분포에 대한 것인지, 두 범주형 변수의 분포의 관계를 검정하는 것인지에 따라 적합성 검정과 독립성 검정으로 나뉘어진다.

각각의 검정은 범주에 대한 기대 관측도수가 충분히 크면-주로 5 이상이면-표준정규분포나 카이제곱 분포 등의 연속형 분포로 근사하여 가설검정을 하고, 기대 관측도수가 충분히 크지 않으면 이항분포, 다항분포, 초기하 분포 등의 이산형 분포를 이용하여 가설검정을 수행한다. 이산형 분포를 이용하는 경우 계산량이 많이 필요할 수 있다. 이 경우 분포를 직접 계산하기 보다는 몬테 카를로 시뮬레이션으로 p-값을 구한다.

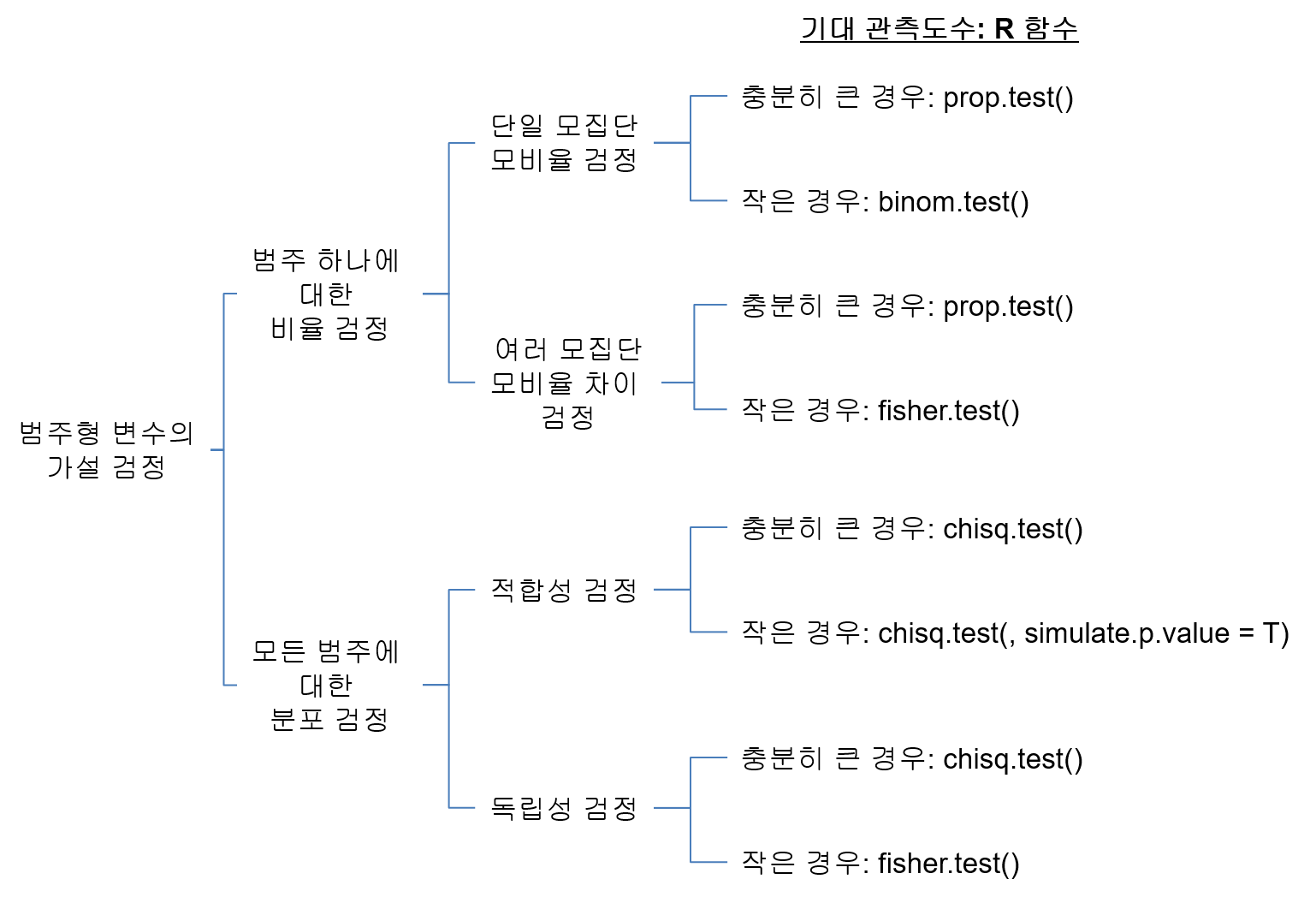
Figure 11.1: 범주형 변수의 가설검정의 종류와 사용해야 할 R 함수

---

8. 이미 요인으로 변경된 범주형 변수는 relevel() 함수를 사용하여 첫 번째 범주를 더 쉽게 지정할 수 있다. 관심 있는 독자는 도움말을 참조하기 바란다.↩︎