Chapter 4 R 데이터 구조
R은 숫자, 문자열, 논리값이라는 데이터 형식을 가지고 더 복잡한 데이터 구조를 만든다. R에서 흔히 사용되는 4가지 데이터 구조는 벡터, 행렬, 리스트, 데이터 프레임이다.
그림 4.1은 벡터, 행렬/배열, 리스트, 데이터 프레임의 구조를 도식화한 것이다. 벡터는 동일한 형식의 데이터를 1차원으로 연결한 데이터 구조이고, 행렬은 동일한 형식의 데이터를 2차원으로, 배열을 2차원 이상의 차원으로 데이터를 연결한 데이터 구조이다. 반면 리스트와 데이터 프레임은 서로 다은 형식의 데이터를 하나의 데이터 구조로 묶어 준다.
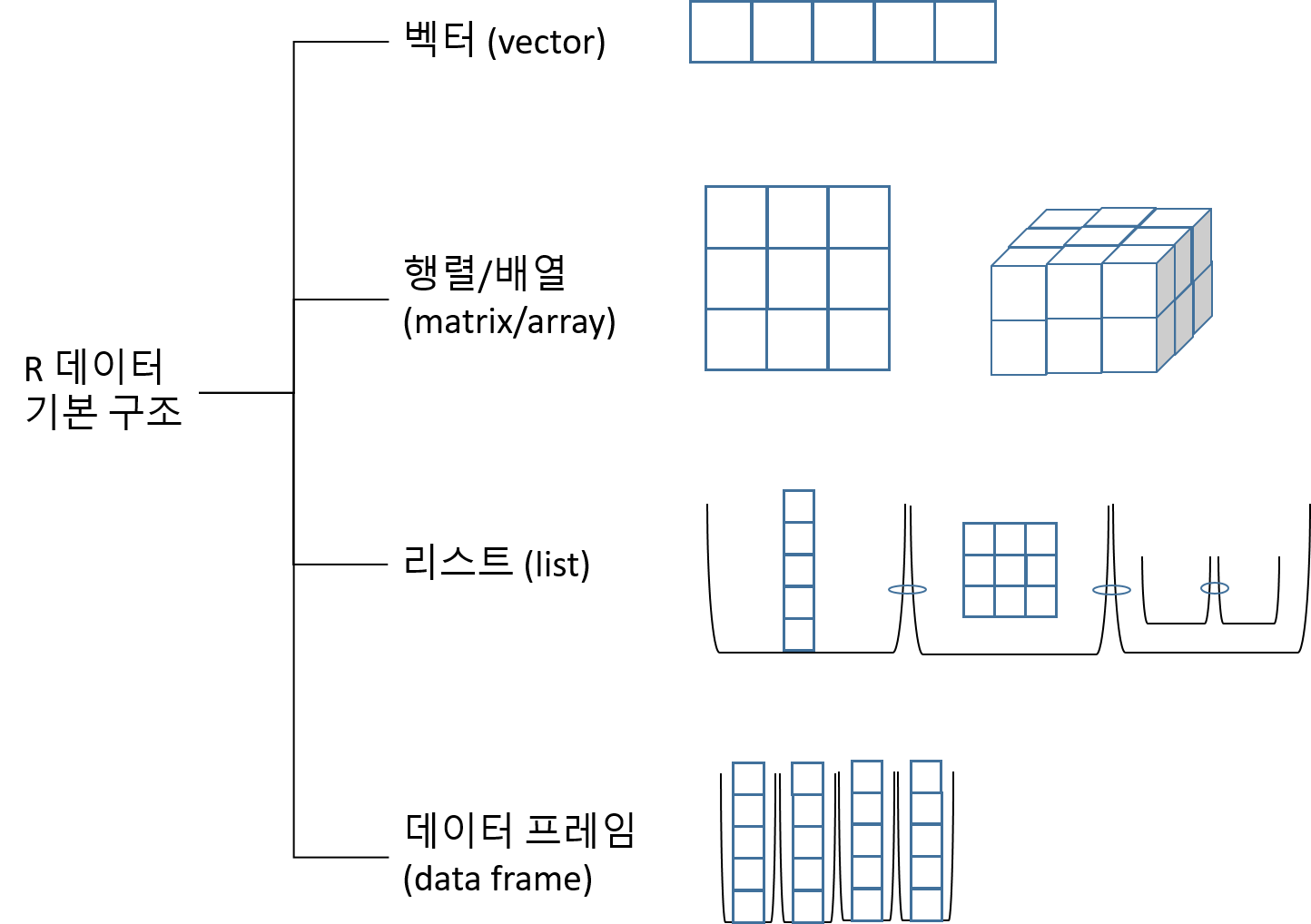
Figure 4.1: R 데이터의 기본 구조
이 책에서는 R 데이터 구조에 대한 문법 중에 벡터와 데이터 프레임에 대한 기본적인 문법만 다루고 나머지 부분은 생략하고자 한다. 통계분석에서 가장 중요한 데이터 구조가 데이터 프레임이므로 데이터 프레임에 대한 기본적인 이해가 필요하고, 데이터 프레임의 각 열은 벡터이므로 벡터에 대한 이해도 필요하기 때문이다. R의 데이터 구조에 대한 좀 더 전반적인 이해를 원하는 독자는 졸저 R 프로그래밍을 참조하기 바란다.
4.1 벡터
벡터는 R의 통계 분석에서 가장 중요한 데이터 형식이다. 다른 범용의 프로그래밍 언어와는 다르게 R은 벡터 단위의 연산 및 조작을 지원함으로써 통계 데이터 분석에 매우 편리한 이점을 제공한다.
4.1.1 벡터는 동일 형식 데이터의 나열
벡터는 50명 학생들의 키 데이터 (162.1, 175.8, 183.2, …), 50명 학생들의 성별 데이터 (“여”, “남”, “남”, …)처럼 한가지 형식의 데이터를 나열한 것이다. 여기서 형식이란 1과 2 등의 숫자 형식, “여”와 “남” 등의 문자열 형식, TRUE와 FALSE의 논리값 형식을 의미한다. 숫자 벡터에는 숫자 데이터만 나열되고, 문자열 벡터나 논리값 벡터에는 각각 문자열과 논리값만이 나열된다.
벡터가 포함하고 있는 데이터의 개수를 벡터의 길이 또는 크기라고 한다. 따라서 50 명 학생의 키 데이터는 길이가 50인 벡터가 된다. 사실 R은 벡터가 아닌 숫자, 문자, 논리값은 없다. 10이라는 숫자 하나도 사실은 길이가 1인 숫자 벡터이고, 문자열도 논리값도 길이가 1인 문자 벡터와 논리 벡터일 뿐이다.
벡터를 사용하기 위해서는 벡터를 생성하는 법, 벡터를 연산하는 법, 벡터의 일부분을 필터링/인덱싱하는 법을 배워야 한다.
4.1.2 벡터를 생성하는 법
4.1.2.1 c() 함수를 이용한 벡터의 생성
벡터는 기본적으로 벡터의 요소를 c() 함수로 연결하여 만든다.
다음 예처럼 1, 3, 5라는 숫자를 차례로 연결하여 벡터를 만들고 싶으면, 다음처럼 c() 함수에 각 요소를 차례로 인수로 기술한다.
[1] 1 3 5다음 예처럼 문자열이나 논리값을 연결하여 문자열 벡터와 논리값 벡터를 만들 수 있다. 아울러 연결하고자 하는 요소의 개수는 원하는 만큼 나열할 수 있다.
[1] "빨강" "파랑" "노랑"[1] TRUE FALSE FALSE TRUEc() 함수는 요소를 하나씩 연결하는 것뿐만 아니라 여러 개의 요소를 가진 벡터들을 연결하여 더 큰 벡터를 만들 수도 있다.
[1] 7 9[1] 1 3 5 7 9[1] 7 9 1 3 5앞의 예는 세 요소를 가진 벡터 x와 두 요소를 가진 벡터 w를 연결하여 새로운 벡터를 만든 예이다. 나열 순서에 따라 새롭게 만들어지는 벡터의 요소들의 위치가 어떻게 되는지 확인해 보라. 이론적으로 말하자면 사실 앞서 본 숫자 1, 3, 5도 요소가 하나인 벡터이고, 요소가 하나짜리 벡터를 연결하여 x와 w라는 벡터를 만든 것이다.
4.1.2.2 수열 패턴을 이용한 숫자 벡터의 생성
1에서부터 10까지의 자연수로 이루어진 벡터를 만든다고 해 보자. 앞에서 배운 c() 함수를 이용하여 이 벡터를 만드려면 10개의 요소를 일일이 나열하여야 하므로 매우 번거로운 작업이 된다. 이럴 때 사용할 수 있는 것이 수열 패턴을 이용하여 숫자 벡터를 만드는 것이다.
: 연산자를 이용하면 다음처럼 하나씩 증가하거나 감소하는 수열 패턴으로 벡터를 만들 수 있다. : 연산자 앞에 기술된 숫자를 시작으로 하여 뒤에 기술된 숫자가 앞에 기술된 숫자보다 크면 하나씩 증가하는, 작으면 감소하는 패턴을 만든다.
[1] 1 2 3 4 5 6 7 8 9 10 [1] 20 19 18 17 16 15 14 13 12 11seq() 함수를 사용하면 수열의 시작점(from)과 종료점(to), 그리고 수열이 얼만큼 증가 또는 감소될 지(by)를 지정할 수 있다.
[1] 1 3 5 7 9[1] 11 22 33 44 55 66 77 88 99[1] 100 85 70 55 40 25 104.1.2.3 비교 연산을 이용한 논리값 벡터 만들기
논리값 벡터는 자주 비교 연산을 이용하여 만들어진다. 예를 들어 중간고사 점수가 80점 이상인 학생은 TRUE, 나머지 학생은 FALSE로 하는 논리값 벡터를 만든다고 해 보자. 다음처럼 학생의 점수가 scores라는 변수에 들어가 있다고 해 보자. 그러면 다음처럼 비교 연산을 이용하여 간단히 논리값 벡터를 만들 수 있다.
[1] 75 92 88 60 80[1] FALSE TRUE TRUE FALSE TRUE[1] FALSE TRUE TRUE FALSE FALSE논리값 연산을 이용하면 더 복잡한 조건의 요소만 TRUE가 되도록 논리값 벡터를 만들 수 있다. 다음은 80점 이상이지만 90점 미만인 학생만 TRUE로 만든 예이다.
[1] FALSE FALSE TRUE FALSE TRUE그런데 앞의 비교 연산의 왼편에 있는 scores는 다섯 개의 요소를 가지고 있지만, 오른편에는 오직 하나의 숫자로만 이루어진 벡터가 있다. R은 연산을 해야 하는 벡터의 길이가 다르면 요소의 재활용이라는 원리를 사용하여 연산을 수행한다. 그러면 벡터의 연산이 어떻게 이루어지는지 살펴보자.
4.1.3 벡터의 연산
R에서 벡터에 대한 연산은 대부분 동일 위치의 요소끼리 그리고 요소의 재활용이라는 두 가지 원칙에 따라 수행된다. 동일 위치의 요소끼리라는 원칙은 동일한 길이의 두 벡터가 연산이 이루어지면 같은 위치의 요소끼리 연산이 이루어 진다는 것이다.
[1] 1 2 3 4 5 6[1] 10 20 30 40 50 60[1] 11 22 33 44 55 66[1] 10 40 90 160 250 360숫자 벡터뿐 아니라 문자열, 논리값 벡터도 같은 원칙에 의해서 연산이 이루어진다.
[1] 1 3 5[1] "빨강" "파랑" "노랑"[1] "빨강-1" "파랑-3" "노랑-5"[1] FALSE FALSE TRUE[1] TRUE FALSE TRUE길이가 같은 벡터는 동일한 위치의 요소끼리 연산이 된다면, 길이가 다른 벡터의 연산을 어떻게 이루어질까? 연산을 해야할 벡터의 길이가 서로 다르면 짧은 길이의 벡터의 요소가 반복적으로 요소 재활용이 되어 길이가 긴 벡터의 길이만큼 늘어난 후, 동일한 위치의 요소끼리 연산이 수행된다.
[1] 11 22 13 24 15 26[1] 1 20 300 4 50 600[1] 1000 2000 3000 4000 5000 6000마지막 연산은 길이가 1인 벡터가 a에 맞추어 6 개의 요소가 되도록 반복되어 재활용된 후 같은 위치의 요소끼리 연산이 이루어졌다. 마찬가지로 앞서 학생들의 점수를 비교 연산한 예에서도 오른편의 숫자가 학생들의 점수의 개수만큼 반복되어 비교가 이루어졌다.
4.1.4 벡터의 필터링/인덱싱
데이터를 분석하다 보면, 데이터의 특정 요소만 추출하여 분석해 보고 싶을 때가 있다. 40세 이상의 고객만 추출하여 분석한다든지, 남자 학생에 대해서만 별도의 분석을 하는 경우가 그러한 예라고 할 수 있다. 이렇게 데이터에서 특정 부분만 추출하여 새로운 데이터를 만드는 작업을 필터링(filtering)이라고 한다.
벡터 필터링은 특정 벡터에서 특정 요소만을 추출하는 것을 의미한다. R에서 벡터 필터링은 인덱스 벡터를 이용하여 수행된다. 여기서 인덱스란 벡터에서 특정 요소의 위치를 의미한다. 예를 들어 5개의 요소로 구성된 벡터에서 두번째 요소를 추출하려면 두번째라는 위치가 그 요소의 인덱스가 된다. 그런데 어떤 벡터에서 추출하고자 하는 요소가 여러 개일 수도 있다. 이 경우 추출해야할 위치를 여러 개 나열해야 하고, 이렇게 나열한 요소의 위치 정보를 인덱스 벡터라고 한다. 물론 하나의 요소만 추출하고자 한다면 인덱스 벡터는 길이가 1이 될 것이다.
벡터 필터링을 하려면 다음처럼 벡터의 이름 다음에 인덱스 벡터를 대괄호 안에 기술하면 된다.
인덱스 벡터는 자연수 벡터, 음의 정수 벡터, 논리값 벡터, 이름 벡터의 네 가지 형태를 가질 수 있다. 이 중에서 자연수, 음의 정수, 논리값 인덱스 벡터를 각각 살펴보도록 하자.
자연수 인덱스 벡터는 벡터에서 뽑아내고자 하는 요소의 위치를 자연수로 기술하는 인덱스 벡터이다. 다음은 학생들의 성적 벡터인 scores 벡터에서 각 위치의 데이터를 뽑아내는 예이다.
[1] 92[1] 92 88 60[1] 75 60음의 정수 인덱스 벡터는 벡터에서 어떤 위치의 요소만 제외하고 뽑을 때 사용하는 인덱스 벡터이다.
[1] 75 88 60 80[1] 92 88 80인덱스 벡터에서 가장 자주 사용되고 유용한 인덱스 벡터가 논리값 인덱스 벡터이다. 논리값 인덱스 벡터는 뽑아내고자 하는 위치의 요소에는 TRUE, 뽑지 않은 위치의 요소에는 FALSE를 기술한다.
[1] 75 88 60자연수 인덱스 벡터나 음의 정수 인덱스 벡터와는 달리 논리값 인덱스 벡터는 벡터의 모든 요소에 TRUE나 FALSE가 기술되어야 한다. 만약 논리 인덱스 벡터의 길이가 원래 벡터보다 짧으면 다음처럼 벡터의 요소의 재활용이 인덱스 벡터에 적용된다.
[1] 75 88 80논리값 인덱스 벡터가 자주 사용되는 이유는 특정 조건에 맞는 요소만 벡터에서 뽑아낼 수 있기 때문이다. 다음은 학생 점수가 80점 이상인 학생의 데이터와 80점 이상이고 90점 미만인 학생의 데이터를 뽑아낸 예이다.
[1] 92 88 80[1] 88 80위의 예에서는 데이터가 5 개밖에 없으므로 자연수 인덱스 벡터를 사용하여도 필터링이 가능하다. 그러나 데이터가 수백, 수천개가 된다고 상상해 보자. 그러면 논리값 인덱스 벡터가 얼마나 유용한 도구인지 쉽게 이해할 수 있을 것이다.
이것으로 벡터에 대한 기본적인 사항을 다루었다. 그렇지만 이는 매우 기본적인 사항이므로 좀 더 복잡한 벡터의 조작이 필요한 독자는 R 프로그래밍의 R 벡터 장을 참조하기 바란다.
마찬가지로 행렬/배열, 리스트, 데이터 프레임 구조에 대해서도 생성, 인덱싱, 연산의 방법을 배워야 한다.
4.2 행렬과 배열
벡터보다 조금 더 복잡한 데이터 구조가 행렬과 배열이다. 행렬과 배열은 벡터처럼 모든 요소가 동일한 데이터의 타입을 가져야 한다.
4.2.1 행렬과 배열은 다차원적 데이터 구조
지금까지 배운 벡터는 일차원적인 데이터 구조였다. 벡터의 길이가 50이라면 벡터의 각 요소의 위치는 \(1, 2, \ldots, 50\)까지 하나의 숫자로 특정할 수 있다. 반면 행렬과 배열은 다차원적인 데이터 구조이다. 행렬은 2차원적 데이터 구조로 행과 열로 구성된다. 행렬의 각 요소의 위치는 어떤 행과 어떤 열에 포함되는지를 나타내는 두 개의 숫자로 특정할 수 있다. 배열은 행렬을 일반화한 것으로 다차원적인 데이터 구조이다. 예로 3차원 배열은 세 개의 숫자에 의해 데이터의 위치를 특정할 수 있다.
4.2.2 행렬과 배열의 필요성
행렬의 예로 다음을 고려해 보자. 어떤 강의의 수강생을 성별, 학년의 두 가지 기준으로 분류한다고 해 보자. 그러면 표 4.1 같은 형식으로 데이터를 정리할 수 있을 것이다. 이와 같이 두 범주형 변수에 대해 관측도수를 요약한 표를 교차표(cross table) 또는 분할표라고 한다.
| 1학년 | 2학년 | 3학년 | 4학년 | |
|---|---|---|---|---|
| 남 | 0 | 5 | 7 | 5 |
| 여 | 2 | 4 | 8 | 2 |
표 4.1 같은 데이터는 일차원적인 벡터 형태로 데이터를 저장하면 각 데이터 요소가 어떤 의미를 갖는지 파악하기가 쉽지 않다. 이러한 경우에는 2차원으로 구성된 행렬을 이용하는 것이 좋다.
통계분석에서 행렬은 주로 시계열 데이터를 다루거나, 빈도표나 분할표(교차표) 등의 표로된 기술통계량을 기술할 때 주로 사용된다. 이 책에서는 시계열 데이터는 다루지 않을 것이며, 빈도표와 분할표도 R 함수의 결과로서만 출력하고 이를 다시 조작하거나 연산하는 작업을 하지 않을 것이므로 행렬에 대한 문법은 더 이상 다루지 않을 것이다. 행렬과 배열에 대한 생성, 연산, 필터링 등의 자세한 문법은 R 프로그래밍의 R 행렬 장을 참조하기 바란다.
4.3 리스트
벡터나 행렬은 포함되는 요소가 모두 같은 타입이어야 했다. 리스트는 숫자와 문자 등 다른 타입의 데이터를 결합시키는 데이터 구조이다. 리스트는 여러 형식의 데이터를 담아두는 데이터 구조로, 리스트의 요소들은 같은 모드나 타입일 필요가 없을 뿐 아니라 리스트 안에 또 다른 리스트를 포함할 수 있다. 따라서 리스트는 컴퓨터의 폴더 구조처럼 계층적 구조를 가질 수 있다.
리스트의 구조는 사용자가 자유롭게 지정할 수 있으므로 매우 복잡한 형식의 데이터를 다룰 수 있다.
4.3.1 리스트 이해의 중요성
실제 데이터 분석을 수행할 때 사용자가 리스트를 직접적으로 생성하는 경우는 그리 많지 않다. 그러나 리스트를 이해하는 것은 매우 중요한데 그 이유는 다음과 같다.
첫째, 데이터 분석에서 가장 중요한 데이터 구조는 데이터 프레임이다. 그리고 데이터 프레임은 리스트를 기반으로 하고 있다. 따라서 데이터 프레임의 근간이 되는 리스트에 대해 명확하게 이해하는 것이 데이터를 효율적으로 조작하는 데 도움이 된다.
둘째, 통계 및 데이터 마이닝을 위해 사용하는 다양한 R의 함수는 복잡한 분석의 결과를 리스트 타입으로 제공하는 경우가 많다. 따라서 데이터 분석의 결과를 효과적으로 이용하기 위해서는 리스트 구조를 이해할 필요가 있다.
리스트에 대한 생성, 연산, 필터링 등의 자세한 문법은 R 프로그래밍의 R 리스트 장을 참조하기 바란다.
4.4 데이터 프레임
데이터 프레임이란 데이터 구조를 다룬다. 보통 다른 통계 소프트웨어에서 데이터 분석의 기본 단위인 데이터 집합 또는 데이터 행렬이라고 불리는 것이다.
데이터 프레임은 행렬을 일반화한 것으로 생각하면 이해하기 쉽다. 행렬에 속한 데이터는 모두 같은 타입인데 반해, 데이터 프레임은 각 열마다 각기 다른 타입의 데이터를 가질 수 있다. 데이터 프레임에는 한 열은 숫자 타입의 데이터가, 다른 한 열은 문자 타입의 데이터가 각각 들어갈 수 있다.
표 1.1처럼 한 강의를 수강하고 있는 학생의 데이터에서 중간고사, 기말고사 같이 숫자 데이터도 있지만, 학생 이름과 성별처럼 문자 데이터도 있다. 데이터의 형태는 다르지만 한 학생에 대한 정보를 얻기 위해서는 숫자, 문자, 논리 값을 포함한 데이터를 다룰 수 있어야 한다. 이 경우에 사용할 수 있는 데이터 구조가 데이터 프레임이라 할 수 있다.
본질적으로 데이터 프레임은 data.frame 클래스인 리스트로서, 각 요소가 벡터이고 벡터의 길이가 같은 리스트이다.
4.4.1 데이터 프레임의 열(변수)은 벡터이다.
표 1.1처럼 한 강의를 수강하고 있는 학생의 데이터에서 각 열은 벡터이다. 성별(gender)은 문자열 벡터이고, 중간고사(mid) 점수는 숫자 벡터이다. 만약 학생 별로 이번 수강이 재수강 여부인지를 TRUE/FALSE로 나타낸다면 논리값 벡터가 될 것이다.
데이터 프레임의 각 열을 선택하는 방법은 다음과 같다.
데이터프레임_이름$열_이름다음은 iris라는 Fisher의 붓꽃 데이터이다. 이 데이터는 150개의 붓꽃에 대한 꽃받침(sepal)과 꽃입(petal)의 길이(length)와 두께(width)와 품종(Species)에 대한 열을 가지고 있다. 다음은 head() 함수로 iris의 앞의 6줄만 확인한 후, 꽃받침의 길이(Sepal.Length) 열을 뽑아낸 결과이다.
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa [1] 5.1 4.9 4.7 4.6 5.0 5.4 4.6 5.0 4.4 4.9 5.4 4.8 4.8 4.3 5.8 5.7 5.4 5.1
[19] 5.7 5.1 5.4 5.1 4.6 5.1 4.8 5.0 5.0 5.2 5.2 4.7 4.8 5.4 5.2 5.5 4.9 5.0
[37] 5.5 4.9 4.4 5.1 5.0 4.5 4.4 5.0 5.1 4.8 5.1 4.6 5.3 5.0 7.0 6.4 6.9 5.5
[55] 6.5 5.7 6.3 4.9 6.6 5.2 5.0 5.9 6.0 6.1 5.6 6.7 5.6 5.8 6.2 5.6 5.9 6.1
[73] 6.3 6.1 6.4 6.6 6.8 6.7 6.0 5.7 5.5 5.5 5.8 6.0 5.4 6.0 6.7 6.3 5.6 5.5
[91] 5.5 6.1 5.8 5.0 5.6 5.7 5.7 6.2 5.1 5.7 6.3 5.8 7.1 6.3 6.5 7.6 4.9 7.3
[109] 6.7 7.2 6.5 6.4 6.8 5.7 5.8 6.4 6.5 7.7 7.7 6.0 6.9 5.6 7.7 6.3 6.7 7.2
[127] 6.2 6.1 6.4 7.2 7.4 7.9 6.4 6.3 6.1 7.7 6.3 6.4 6.0 6.9 6.7 6.9 5.8 6.8
[145] 6.7 6.7 6.3 6.5 6.2 5.9데이터 프레임의 열은 벡터라고 했다. 그러므로 $ 연산자로 데이터 프레임의 열을 지정하면, 데이터 프레임의 열을 벡터처럼 사용할 수 있다. 앞에서 본 꽃받침의 길이(iris$Sepal.Length)는 숫자 벡터이다. 그러므로 숫자 벡터에 사용되는 평균과 표준편차를 구하는 함수인 mean()과 sd() 함수를 사용할 수 있고, 숫자 벡터에서 배운 연산, 필터링을 사용할 수 있다.
[1] 5.843333[1] 0.8280661 [1] 7.1 7.6 7.3 7.2 7.7 7.7 7.7 7.2 7.2 7.4 7.9 7.7한 가지 주의할 점은, 앞으로 볼 R의 통계분석을 위한 함수들이 사용자의 편의를 위해 분석에 사용할 데이터 프레임을 data 또는 .data 등의 인수로 지정한 후, 이 데이터 프레임의 열을 함수 안에서 지정할 때 $ 연산자를 사용하지 않고 열의 이름만 지정하여 사용하는 경우가 있다. 예를 들어 xtab() 함수는 빈도표나 교차표를 구할 때 사용하는데, 다음처럼 data 인수에 데이터 프레임을 지정한 후 빈도를 구할 열을 $ 연산자 없이 지정하고 있다.
Species
setosa versicolor virginica
50 50 50 그러나 이처럼 data 등의 인수로 함수에서 사용할 데이터 프레임을 명확하게 지정한 경우가 아니면, 데이터 프레임의 열은 항상 $ 연산자를 사용하여 지정해야 한다. 다음은 table() 함수를 사용하여 동일한 빈도표를 구한 경우이다.
setosa versicolor virginica
50 50 50 다시 말해 데이터 프레임의 열은 $ 연산자로 지정하는 것이 원래의 문법이나, 데이터 프레임을 사용하는 많은 함수들이 사용자의 편의를 위해 data 인수에 이미 데이터 프레임을 지정했으면, 열의 이름만으로 열을 지정하도록 편의를 제공하고 있지만, 그렇지 않은 함수들도 있으므로 표준적인 문법과 편의 기능을 서로 혼동하지 말아야 한다는 것이다.
4.4.2 데이터프레임을 행렬 형식으로 필터링
행렬 형식으로 필터링은 2차원 인덱스 구조를 갖는다.
데이터 프레임은 열의 길이가 모두 같기 때문에, 보통의 리스트에는 없는 행렬과 같은 필터링 방법이 존재한다. 특히 기존의 데이터 프레임에 행을 삭제 또는 추가할 필요가 있는 경우 이러한 행렬 방식의 필터링 방법은 매우 유용한다.
데이터 프레임의 인덱스 벡터의 사용은 다음과 같이 행렬처럼 행과 열을 독립적으로 지정하는 2차원 인덱스 구조를 가진다.
다음은 iris 데이터 프레임에서 행렬 인덱스 벡터를 이용하여 데이터의 일부를 지정한 예이다. 행과 열의 인덱스 벡터를 비워두면 모든 행이나 열을 지정한다. 행과 열의 인덱스 벡터에 자연수 인덱스 벡터, 음의 정수 인덱스 벡터, 논리값 인덱스 벡터, 문자열 인덱스 벡터를 지정하면 해당되는 행과 열이 지정된다.
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa Sepal.Length Sepal.Width Petal.Length Petal.Width Species
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
7 4.6 3.4 1.4 0.3 setosa
8 5.0 3.4 1.5 0.2 setosa
9 4.4 2.9 1.4 0.2 setosa
10 4.9 3.1 1.5 0.1 setosa
11 5.4 3.7 1.5 0.2 setosa
12 4.8 3.4 1.6 0.2 setosa
13 4.8 3.0 1.4 0.1 setosa
14 4.3 3.0 1.1 0.1 setosa
15 5.8 4.0 1.2 0.2 setosa
16 5.7 4.4 1.5 0.4 setosa
17 5.4 3.9 1.3 0.4 setosa
18 5.1 3.5 1.4 0.3 setosa
19 5.7 3.8 1.7 0.3 setosa
20 5.1 3.8 1.5 0.3 setosa
21 5.4 3.4 1.7 0.2 setosa
22 5.1 3.7 1.5 0.4 setosa
23 4.6 3.6 1.0 0.2 setosa
24 5.1 3.3 1.7 0.5 setosa
25 4.8 3.4 1.9 0.2 setosa
26 5.0 3.0 1.6 0.2 setosa
27 5.0 3.4 1.6 0.4 setosa
28 5.2 3.5 1.5 0.2 setosa
29 5.2 3.4 1.4 0.2 setosa
30 4.7 3.2 1.6 0.2 setosa
31 4.8 3.1 1.6 0.2 setosa
32 5.4 3.4 1.5 0.4 setosa
33 5.2 4.1 1.5 0.1 setosa
34 5.5 4.2 1.4 0.2 setosa
35 4.9 3.1 1.5 0.2 setosa
36 5.0 3.2 1.2 0.2 setosa
37 5.5 3.5 1.3 0.2 setosa
38 4.9 3.6 1.4 0.1 setosa
39 4.4 3.0 1.3 0.2 setosa
40 5.1 3.4 1.5 0.2 setosa
41 5.0 3.5 1.3 0.3 setosa
42 4.5 2.3 1.3 0.3 setosa
43 4.4 3.2 1.3 0.2 setosa
44 5.0 3.5 1.6 0.6 setosa
45 5.1 3.8 1.9 0.4 setosa
46 4.8 3.0 1.4 0.3 setosa
47 5.1 3.8 1.6 0.2 setosa
48 4.6 3.2 1.4 0.2 setosa
49 5.3 3.7 1.5 0.2 setosa
50 5.0 3.3 1.4 0.2 setosa
51 7.0 3.2 4.7 1.4 versicolor
52 6.4 3.2 4.5 1.5 versicolor
53 6.9 3.1 4.9 1.5 versicolor
54 5.5 2.3 4.0 1.3 versicolor
55 6.5 2.8 4.6 1.5 versicolor
56 5.7 2.8 4.5 1.3 versicolor
57 6.3 3.3 4.7 1.6 versicolor
58 4.9 2.4 3.3 1.0 versicolor
59 6.6 2.9 4.6 1.3 versicolor
60 5.2 2.7 3.9 1.4 versicolor
61 5.0 2.0 3.5 1.0 versicolor
62 5.9 3.0 4.2 1.5 versicolor
63 6.0 2.2 4.0 1.0 versicolor
64 6.1 2.9 4.7 1.4 versicolor
65 5.6 2.9 3.6 1.3 versicolor
66 6.7 3.1 4.4 1.4 versicolor
67 5.6 3.0 4.5 1.5 versicolor
68 5.8 2.7 4.1 1.0 versicolor
69 6.2 2.2 4.5 1.5 versicolor
70 5.6 2.5 3.9 1.1 versicolor
71 5.9 3.2 4.8 1.8 versicolor
72 6.1 2.8 4.0 1.3 versicolor
73 6.3 2.5 4.9 1.5 versicolor
74 6.1 2.8 4.7 1.2 versicolor
75 6.4 2.9 4.3 1.3 versicolor
76 6.6 3.0 4.4 1.4 versicolor
77 6.8 2.8 4.8 1.4 versicolor
78 6.7 3.0 5.0 1.7 versicolor
79 6.0 2.9 4.5 1.5 versicolor
80 5.7 2.6 3.5 1.0 versicolor
81 5.5 2.4 3.8 1.1 versicolor
82 5.5 2.4 3.7 1.0 versicolor
83 5.8 2.7 3.9 1.2 versicolor
84 6.0 2.7 5.1 1.6 versicolor
85 5.4 3.0 4.5 1.5 versicolor
86 6.0 3.4 4.5 1.6 versicolor
87 6.7 3.1 4.7 1.5 versicolor
88 6.3 2.3 4.4 1.3 versicolor
89 5.6 3.0 4.1 1.3 versicolor
90 5.5 2.5 4.0 1.3 versicolor
91 5.5 2.6 4.4 1.2 versicolor
92 6.1 3.0 4.6 1.4 versicolor
93 5.8 2.6 4.0 1.2 versicolor
94 5.0 2.3 3.3 1.0 versicolor
95 5.6 2.7 4.2 1.3 versicolor
96 5.7 3.0 4.2 1.2 versicolor
97 5.7 2.9 4.2 1.3 versicolor
98 6.2 2.9 4.3 1.3 versicolor
99 5.1 2.5 3.0 1.1 versicolor
100 5.7 2.8 4.1 1.3 versicolor
101 6.3 3.3 6.0 2.5 virginica
102 5.8 2.7 5.1 1.9 virginica
103 7.1 3.0 5.9 2.1 virginica
104 6.3 2.9 5.6 1.8 virginica
105 6.5 3.0 5.8 2.2 virginica
106 7.6 3.0 6.6 2.1 virginica
107 4.9 2.5 4.5 1.7 virginica
108 7.3 2.9 6.3 1.8 virginica
109 6.7 2.5 5.8 1.8 virginica
110 7.2 3.6 6.1 2.5 virginica
111 6.5 3.2 5.1 2.0 virginica
112 6.4 2.7 5.3 1.9 virginica
113 6.8 3.0 5.5 2.1 virginica
114 5.7 2.5 5.0 2.0 virginica
115 5.8 2.8 5.1 2.4 virginica
116 6.4 3.2 5.3 2.3 virginica
117 6.5 3.0 5.5 1.8 virginica
118 7.7 3.8 6.7 2.2 virginica
119 7.7 2.6 6.9 2.3 virginica
120 6.0 2.2 5.0 1.5 virginica
121 6.9 3.2 5.7 2.3 virginica
122 5.6 2.8 4.9 2.0 virginica
123 7.7 2.8 6.7 2.0 virginica
124 6.3 2.7 4.9 1.8 virginica
125 6.7 3.3 5.7 2.1 virginica
126 7.2 3.2 6.0 1.8 virginica
127 6.2 2.8 4.8 1.8 virginica
128 6.1 3.0 4.9 1.8 virginica
129 6.4 2.8 5.6 2.1 virginica
130 7.2 3.0 5.8 1.6 virginica
131 7.4 2.8 6.1 1.9 virginica
132 7.9 3.8 6.4 2.0 virginica
133 6.4 2.8 5.6 2.2 virginica
134 6.3 2.8 5.1 1.5 virginica
135 6.1 2.6 5.6 1.4 virginica
136 7.7 3.0 6.1 2.3 virginica
137 6.3 3.4 5.6 2.4 virginica
138 6.4 3.1 5.5 1.8 virginica
139 6.0 3.0 4.8 1.8 virginica
140 6.9 3.1 5.4 2.1 virginica
141 6.7 3.1 5.6 2.4 virginica
142 6.9 3.1 5.1 2.3 virginica
143 5.8 2.7 5.1 1.9 virginica
144 6.8 3.2 5.9 2.3 virginica
145 6.7 3.3 5.7 2.5 virginica
146 6.7 3.0 5.2 2.3 virginica
147 6.3 2.5 5.0 1.9 virginica
148 6.5 3.0 5.2 2.0 virginica
149 6.2 3.4 5.4 2.3 virginica
150 5.9 3.0 5.1 1.8 virginica Sepal.Width Petal.Width
1 3.5 0.2
2 3.0 0.2
3 3.2 0.2
4 3.1 0.2
5 3.6 0.2 Sepal.Length Sepal.Width Petal.Length Species
1 5.1 3.5 1.4 setosa
2 4.9 3.0 1.4 setosa
3 4.7 3.2 1.3 setosa
4 4.6 3.1 1.5 setosa
5 5.0 3.6 1.4 setosa Sepal.Length Sepal.Width Petal.Length Petal.Width Species
103 7.1 3.0 5.9 2.1 virginica
106 7.6 3.0 6.6 2.1 virginica
108 7.3 2.9 6.3 1.8 virginica
110 7.2 3.6 6.1 2.5 virginica
118 7.7 3.8 6.7 2.2 virginica
119 7.7 2.6 6.9 2.3 virginica
123 7.7 2.8 6.7 2.0 virginica
126 7.2 3.2 6.0 1.8 virginica
130 7.2 3.0 5.8 1.6 virginica
131 7.4 2.8 6.1 1.9 virginica
132 7.9 3.8 6.4 2.0 virginica
136 7.7 3.0 6.1 2.3 virginica Petal.Length Petal.Width Species
103 5.9 2.1 virginica
106 6.6 2.1 virginica
108 6.3 1.8 virginica
110 6.1 2.5 virginica
118 6.7 2.2 virginica
119 6.9 2.3 virginica
123 6.7 2.0 virginica
126 6.0 1.8 virginica
130 5.8 1.6 virginica
131 6.1 1.9 virginica
132 6.4 2.0 virginica
136 6.1 2.3 virginica4.4.3 데이터 프레임의 문법과 조작
데이터 프레임의 생성, 연산, 필터링하는 R의 기본 문법을 더 자세히 알고자 하면, R 프로그래밍의 R 데이터 프레임 장을 참조하기 바란다.
앞서 언급하였듯이 데이터 프레임은 데이터 분석에서 가장 중요한 데이터 구조이다. 그렇기 때문에 분석에 적절하게 데이터 프레임을 변형하거나 결합하는 작업이 데이터 전처리에서 빈번하게 이루어진다. 이 때 데이터 프레임의 생성, 연산, 필터링하는 R의 기본 문법을 사용하여도 데이터 프레임을 조작할 수 있지만, 최근의 추세는 Hadley Wickham 등이 제공하고 있는 tidyverse 패키지를 사용하는 경우가 많다. tidyverse 패키지를 사용하여 데이터 프레임을 조작하는 방법을 알고자 하는 독자는 R 프로그래밍의 dplyr을 이용한 데이터 변환과 R 고급 데이터 변환 장을 참조하기 바란다.